Clique na imagem
Bons Estudos
Função" foi introduzido por Gottfried Leibniz em 1694, para designar qualquer das várias variáveis geométricas associadas com uma dada curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas às curvas são atualmente chamadas funções diferenciáveis e são ainda o tipo de funções mais encontrado por não-matemáticos. Para este tipo de funções, pode-se falar em limites e derivadas; ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal.
A palavra função foi, posteriormente, usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos (por exemplo, y = F(x)). Ampliando a definição de funções, os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.
Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz (veja aritmetização da análise). Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria dos conjuntos, e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. FoiDirichlet quem criou a definição "formal" de função moderna.
Na definição de Dirichlet, uma função é um caso especial de uma relação. Relação é um conjunto de pares ordenados, onde cada elemento do par pertence a um dos conjuntos relacionados. Nas relações não existem restrições quanto à lei de correspondência entre os elementos dos conjuntos, já para as funções é costume introduzir restrições. Na maioria dos casos de interesse prático, entretanto, as diferenças entre as definições moderna e de Euler são desprezáveis.
Conceito
O conceito de uma função é uma generalização da noção comum de "fórmula matemática". Funções descrevem relações matemáticasespeciais entre dois objetos, x e y=f(x). O objeto x é chamado o argumento ou domínio da função f e o objeto y que depende de x é chamado imagem de x pela f.
Intuitivamente, uma função é uma maneira de associar a cada valor do argumento x um único valor da função f(x). Isto pode ser feito especificando através de uma fórmula, um relacionamento gráfico entre diagramas representando os dois conjuntos, e/ou uma regra de associação ou mesmo uma tabela de correspondência pode ser construída; entre conjuntos numéricos é comum representarmos funções por seus gráficos, cada par de elementos relacionados pela função determina um ponto nesta representação, a restrição de unicidade da imagem implica um único ponto da função em cada linha de chamada do valor independente x.
Este conceito é determinístico, sempre produz o mesmo resultado a partir de uma dada entrada (a generalização aos valores aleatórios é chamada de função estocástica). Uma função pode ser vista como uma "máquina" ou "caixa preta" que converte entradas válidas em saídasde forma unívoca, por isso alguns autores chamam as funções de relações unívocas.
O tipo de função mais comum é aquele onde o argumento e o valor da função são ambos numéricos, o relacionamento entre os dois é expresso por uma fórmula e o valor da função é obtido através da substituição direta dos argumentos. Considere o exemplo
Que resulta em qualquer valor de x ao quadrado.
Uma generalização direta é permitir que funções dependam não só de um único valor, mas de vários. Por exemplo,
recebe dois números x e y e resulta no produto deles, xy.
De acordo com o modo como uma função é especificada, ela pode ser chamada de função explícita (exemplo acima) ou de função implícita, como em
que implicitamente especifica a função
A noção intuitiva de funções não se limita a computações usando apenas números. A noção matemática de funções é bem mais ampla. Assim, uma função liga um domínio (conjunto de valores de entrada) com um segundo conjunto o contra-domínio (ou codomínio) de tal forma que a cada elemento do domínio está associado exactamente um elemento do contra-domínio. O conjunto dos elementos do contra-domínio que são relacionados pela f a algum x do domínio, é chamado de "conjunto-imagem" ou "imagem".
As funções são definidas abstractamente por certas relações. Por causa de sua generalização as funções aparecem em muitos contextos matemáticos e muitas áreas desta ciência baseiam-se no estudo de funções. Pode notar-se que as palavras "função", "mapeamento", "mapear" e "transformar" são geralmente usadas como termos equivalentes. Além disso funções podem ocasionalmente ser referidas comofunções bem definidas ou função total.
Assista aos vídeos:
Tipo de função
característica deste tipo de função Conjunto imagem Explicação visual Exemplo Admite Função inversa?/ é inversível? Funções injectoras (ou injectivas) Cada elemento da imagem (da saída) está associado a apenas um elemento do domínio (da entrada), isto é uma relação um para um entre os elementos do domínio e daimagem. Isto é, quando 
no domínio então 
no contradomínio. A cardinalidade docontra-domínio é sempre maior ou igual à do domínio em uma função inje(c)tora. Maior ou igual ao contradomínio (ou seja, podem haver mais elementos nocontra-domínioque no conjunto imagem da função). 
f: N --> N dada por f(x) = 2x (é injetiva porque, sempre que tomamos dois valores diferentes de x (digamos a e b), obtemos valores diferentes para f(x) (digamos f(a)≠f(b)). Notar que esta funçãonão é sobrejetiva. Não necessariamente, , mas sempre admite inversa à esquerda. Funções sobrejetoras (ou sobrejetiva) Todos os elementos do contra-domínio (da saída) estão associados a algum elemento do domínio (da entrada). Igual ao conjunto contra-domínio 
A função f:R→R definida por f(x)=6x não é sobrejetora, pois o número -1 é elemento do contradomínio R e não é imagem de qualquer elemento do domínio. Não necessariamente, , mas sempre admite inversa à direita. Funções bijetoras (ou bijetiva) São ao mesmo tempo sobrejetoras e injetoras, isto é, todos os elementos do domínio estão associados a todos os elementos do contra-domínio de forma um para um e exclusiva. Igual ao conjunto contra-domínio 
função identidade Sim, sempre; imagem (=contra-domínio, neste caso) vira domínio e vice-versa.
Exercícios:Por: Info Vestibulares
Sejam f e g funções de R em R, sendo R o conjunto dos números reais, dadas porf(x) = 2x - 3 e f(g(x)) = -4x + 1. Nestas condições, g(-1) é igual a:a) -5b) -4c) 0d) 4e) 5
O maior valor assumido pela função y = 2 - ½ x - 2½ é:a) 1b) 2c) 3d) 4e) 5
O gráfico da função f de R em R, dada por f(x) = ½ 1 - x½ - 2, intercepta o eixo dasabcissas nos pontos (a,b) e (c,d). Nestas condições o valor de d + c - b - a é:a) 4b) -4c) 5d) -5e) 0
Se f (g (x) ) = 5x - 2 e f (x) = 5x + 4 , então g(x) é igual a:a) x - 2b) x - 6c) x - 6/5d) 5x - 2e) 5x + 2
Chama-se ponto fixo de uma função f a um número x tal que f(x) = x. Se o ponto fixo dafunção f(x) = mx + 5 é igual a 10, então podemos afirmar que o módulo do décuplo do ponto fixo dafunção g(x) = 2x - m é igual a:a) 5b) 4c) 3d) 2e) 1
A imagem da função f(x) = (4x + 2) / 3 é (-¥ , 5] , para todo x pertencente a R tal que:a) x£ 13/4b) x< 3/4c) x£ 3/4d) x< 17/4e) x< 11
Seja f : R ® R , uma função tal que f ( x ) = k.x - 1. Se f [ f ( 2 ) ] = 0 e f é estritamentedecrescente, o valor da k-ésima potência de 2 é igual aproximadamente a:a) 0,500b) 0,866c) 0,125d) 0,366e) 0,707
Seja f(x) = ax + b; se os pares ordenados (1,5)Î f e (2,9) Î f então podemos afirmarque o valor do produto (a + b) (10a + 5b) é igual a:a) 225b) 525c) 255d) 100e) 1000
A função f é tal que f(2x + 3) = 3x + 2. Nestas condições, f(3x + 2) é igual a:a) 2x + 3b) 3x + 2c) (2x + 3) / 2d) (9x + 1) /2e) (9x - 1) / 3
Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar quea igualdade gof(x) = fog(x) ocorrerá se e somente se:a) b(1 - c) = d(1 - a)b) a(1 - b) = d(1 - c)c) ab = cdd) ad = bce) a = bc
O conjunto imagem da função y = 1 / (x - 1) é o conjunto:a) R - { 1 }b) [0,2]c) R - {0}d) [0,2)e) (-¥ ,2]
Dadas as proposições:p: Existem funções que não são pares nem ímpares.q: O gráfico de uma função par é uma curva simétrica em relação ao eixo dos y.r: Toda função de A em B é uma relação de A em B.s: A composição de funções é uma operação comutativa.t: O gráfico cartesiano da função y = x / x é uma reta.Podemos afirmar que são falsas:a)nenhumab) todasc) p,q e rd) s e te) r, s e t
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somentese k for igual a:a) -1/3b) 1/3c) 0d) 1e) -1
Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:a) 2 - 2xb) 3 - 3xc) 2x - 5d) 5 - 2xe) uma função par.
Sendo f e g duas funções definidas por f(x) = 6 - 2x e g(x) = 4 -x e sabendo-se quepara " x ¹ 4 , f(x) / g(x) ³ 2, então:a) x³ 4b) x< 4c) x> 4d) x = 4e) x£ 4
Seja a função definida por f(x) = (2x - 3) / 5x. O elemento do domínio de f que tem-2/5 como imagem é:a) 0b) 2/5c) -3d) 3/4e) 4/3
A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemosafirmar que f(1) é igual a:a) 2b) -2c) 0d) 3e) -3
Se f(x) = 1 - 1/x , com x ¹ 0 , então determine o valor deR = 96. f(2) . f(3) . f(4) . ... . f(14) . f(15) . f(16).Resp: 6
A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemosafirmar que f(1) é igual a:a) 2b) -2c) 0d) 3e) -3
Se f(x) = 1/[x(x+1)] com x¹ 0 e x¹ -1, então o valor de S = f(1) + f(2) + f(3) + ... + f(100)é:a)100b) 101c) 100/101d) 101/100e) 1
Uma função real é tal que f(x). f(y) = f(x + y) , f(1) = 3 e f(Ö 3) = 4. O valor de f(2 + Ö 3)é:a) 18b) 24*c) 36d) 42e) 48
Sendo f uma função definida por f(x - 1) = 2 . f(x) + f(x + 1) , tal que f(0) = 2 ef(1) = -1 , o valor de ½ f(3) ½ é:01) 102) 303) 1604) 805) 9
Seja f uma função de N em N , tal que f(0) = -1 , f(1) = 1 e f(n-2) = f(n) . f(n-1),se n³ 2. O conjunto imagem de f é:a) Nb) N - {0}c) {-2,-1,0,1,2}d) {-1,0,1}e) {-1,1}
Sendo f(x) = 100x + 3 , o valor de [f(10-8) - f(103)] / (10-8 - 103) é:a) 10000b) 100c) 10d)10-5e) 10-11 .
Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto (-1 , 8) pertenceao gráfico dessa função, então:a) o seu valor máximo é 1,25b) o seu valor mínimo é 1,25c) o seu valor máximo é 0,25d) o seu valor mínimo é 12,5e) o seu valor máximo é 12,5.
Que número excede o seu quadrado o máximo possível?a) 1/2b) 2c) 1d) 4e) -1/2
A diferença entre dois números é 8. Para que o produto seja o menor possível, umdeles deve ser:a) 16b) 8c) 4d) -4e) -16
A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:a) 16b) 8c) 4d) -4e) -16
Se x1 e x2 são os zeros da função y = 3x2 + 4x - 2 , então o valor de 1/x1 + 1/x2 é iguala:a) 1/8b) 8/3c) 1d) 2e) 3
Gabarito Funções01 D 16 D02 B 17 A03 A 18 604 C 19 A05 A 20 C06 A 21 C07 E 22 E08 A 23 E09 D 24 B10 A 25 E11 C 26 A12 D 27 C13 A 28 E14 D 29 D15 C
29 – (UEFS)
28 - (INFO)
27 - (INFO)
26 - (INFO)
25 – (UCSal)
24 – (UFBA)
23 – (UCSal-95)
22 – (UEFS-95/1)
21 – (UEFS)
20 - (INFO)
19 - (INFO)
18 - (INFO)
17 - (INFO)
16 – (PUC-RS)
15 - (INFO)
14 - (INFO)
13 - (INFO)
12 - (INFO)
11 - (INFO)
10 - (INFO)
9 - (INFO)
8 - (INFO)
7 - (INFO)
6 (UEFS)
5 – (INFO)
4 – (UFBA)
3 – (UCSal)
2 – (UCSal)
1 – (UCSal)
Explicitando conjuntos- Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir a relação R em A×B que está apresentada no gráfico.
Qual resposta mostra a relação R de forma explicita?a. R={(a,1),(b,3),(c,4),(a,3)}
b. R={(1,a),(4,a),(3,b),(c,2)}
c. R={(a,1),(b,3),(c,2)}
d. R={(a,1),(a,4),(b,3),(c,2)}
- Com a mesma relação R do exercício anterior, qual das alternativas é a relação inversa R-1?
- R-1={(a,1),(a,4),(b,3),(c,2)}
- R-1={(1,a),(4,a),(3,b),(2,c)}
- R-1={(4,a),(2,c),(3,b)}
- R-1={(1,a),(2,c)}
- Sejam os conjuntos A={a,b,c,d,e} e B={2,4,6,8,10} e a relação R, mostrada no gráfico.
Quais são as formas explícitas da relação R e da relação inversa R-1?
- Sejam os conjuntos A={1,2,3} e B={1,3,4,5} de números reais e a relação definida por R={(x,y)
A×B: y=2x-1}. Qual dos gráficos cartesianos abaixo, representa a relação R?
- Sejam os conjuntos A={1,3,4,5} e B={0,6,12,20} e a relação R={(x,y) em A×B: y=x(x-1)} definida sobre A×B. Escrever R de uma forma explicita e construir o gráfico cartesiano desta relação.
- Seja A={1,2,3,5,7}. Analisar o gráfico cartesiano da relação R em A×A e responder às questões pertinentes a esta relação.
Qual das alternativas abaixo é verdadeira?- (2,3)
R, (5,1)R, (7,7)R
- (1,1)R, (3,5)R, (5,1)R
- (1,1)R, (5,5)R, (3,5)R
- (2,3)R, (3,5)R, (7,7)R
Dominio, contradominio, imagem, relações direta e inversa- Para a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} definida sobre o conjunto A={1,2,3,5,7}, responda qual das alternativas abaixo representa o contradomínio da relação R. (Dica: Ver o gráfico do Exercício 6)
a. CoDom(R)={1,2,3,5,7}
b. CoDom(R)={1,3,5,7}
c. CoDom(R)=R
d. CoDom(R)={3,5,7}
- Seja a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} def. sobre A={1,2,3,5,7}. Qual alternativa representa o domínio de R. (Dica: Ver o gráfico do Exercício 6)
a. Dom(R)=R
b. Dom(R)={2,5,7}
c. Dom(R)={1,2,7}
d. Dom(R)={1,2,3,5,7}
- Para a relação R={(1,1),(2,3),(3,7),(5,1),(7,7)} def. sobre A={1,2,3,5,7}, qual das alternativas representa a imagem de R. (Dica: Ver o gráfico do Exercício 6)
a. Im(R)={1,2,3,5,7}
b. Im(R)={1,3,5,7}
c. Im(R)={1,3,5}
d. Im(R)=R
- Sejam A={2,4,6,8}, B={1,3,5,7} e a relação R em A×B apresentada pelo seu gráfico cartesiano.
Identifique se cada afirmação é V (verdadeira) ou F (falsa).a. (2,1) pertence à relação R.
b. (3,2) pertence à relação R.
c. (4,3) pertence à relação R.
d. (5,6) pertence à relação R.
e. (8,7) pertence à relação R.
- Usando as informações do exercício anterior, apresente o contradomínio da relação R e a inversa da relação R, denotada por R-1.
Neste trabalho, o conjunto dos números naturais será denotado por N={1,2,3,4,5,6,7,...}.
- Seja a relação R={(x,y)N×N: 2x+y=8}. Qual dos ítens representa o domínio da relação R?
a. {8} b. N c. {1,2,3} d. {2,4,6}
- Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das respostas abaixo representa o contradomínio de R?
a. {1,3,5,7} b. {0,1,2,3,4,5,6,7} c. {0,2,4,6} d. N
- Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das alternativas abaixo representa a imagem de R?
a. {1,3,5,7} b. {2,4,6} c. Ø d. N
- Seja a relação R={(x,y) em N×N: 2x+y=8}. A relação inversa denotada por R-1 está indicada em qual das alternativas?
a. {(6,1),(4,2),(2,3)}
b. Ø
c. {(1,6),(2,4),(3,2)}
d. N
Relações reflexivas, simétricas, transitivas e anti-simétricas- Seja A={1,3,8} e as relações abaixo, definidas sobre A. Quais das alternativas indicam a ocorrência da propriedade reflexiva?
a. R1={(1,1),(1,3),(3,3),(3,1),(8,1)}
b. R2={(1,1),(3,1),(1,8),(3,3),(8,8)}
c. R3={(3,1),(3,3),(5,8),(1,1),(8,8)}
d. R4={(8,8),(3,3),(1,8),(3,1),(1,1)}
e. R5={(8,8),(3,3)}
- Dadas as relações definidas sobre C={1,3,5}, qual delas alternativas mostra uma relação simétrica?
a. R1={(1,3),(5,3),(5,5),(3,5)}
b. R2={(1,3),(3,1),(5,5),(1,5)}
c. R3={(3,1),(3,3),(5,5),(5,1)}
d. R4={(1,1),(3,3),(5,5)}
- A relação R={(1,3),(3,3),(2,4),(3,1),(2,3),(3,2)} def. sobre A={1,2,3,4,5} é simétrica?
- Sejam as relações definidas nos conjuntos indicados. Qual delas é uma relação transitiva?
a. Ra={(2,6),(6,8),(8,2)},conjunto A={2,6,8}.
b. Rb={(1,3),(3,4),(1,2)},conjunto B={1,2,3,4}.
c. Rc={(1,3),(3,5),(1,5)},conjunto C={1,3,5}.
d. Rd={(1,2),(2,3),(3,2)},conjunto D={1,2,3}.
- Dado o conjunto A={1,3,8} e as relações sobre A listadas abaixo, indique qual alternativa mostra uma relação anti-simétrica. Justifique porque as outras relações não são anti-simétricas.
a. R1={(1,3),(3,1),(8,1)}
b. R2={(1,8),(8,8),(1,3),(8,1)}
c. R3={(3,3),(1,8),(8,8),(8,1)}
d. R4={(8,8),(1,3),(8,1),(1,1)}
Definição de função- Quais dos diagramas abaixo se encaixa na definição de função de A em B, onde A={a,b,c} e B={1,2,3}.
- Quais dos diagramas abaixo não representa uma função de A em B, onde A={a,b,c} e B={1,2,3}.
- Dada a função real f(x)=2x+3 definida sobre o conjunto A={1,2,3,4}, apresente o conjunto de todos os pares ordenados pertencentes à função f.
- Dada a função f:R
R definida por:
determinar: f(0), f(-4), f(2) e f(10).
- Qual conjunto é formado pelos valores f(0), f(-3), f(2) e f(10), se a função de R×R está definida por f(x)=x²-4x+7?
a. {67,3,4,7}
b. {0,-3,2,10}
c. {7,28,3,67}
d. {10,2,-3,0}
- Calcular os valores: f(3), f(1), f(0) e f(-10), para a função real f=f(x) definida por:
Zeros de funções- Por definição, zero de uma função é o ponto do domínio de f onde a função se anula. Dadas as quatro funções:f(x)=3x-8, g(x)=2x+6, h(x)=x-1 e i(x)=15x-30qual dos conjuntos contém os zeros de todas as funções.
a. {-8,2,-1,-30}
b. {8/3,-3,1,2}
c. {-8/3,2,-1,-2}
d. {2,8/3,3,30}
- Se uma função do primeiro grau é da forma f(x)=ax+b tal que b=-11 e f(3)=7, obtenha o valor da constante a.
- Usando f(x)=ax+b e sabendo-se que f(-2)=8 e f(-1)=2, obter os valores de a e b.
- Obter a função f(x)=ax+b tal que f(-3)=9 e f(5)=-7. Obtenha f(1) e o zero desta função.
- Para a função real definida por f(x)=x²+2x-3, obtenha: f-1(5), f-1(0), f-1(-3) e f-1(x+3)
- Para a função real f(x)=2x+4, qual é o conjunto f-1(8)?
- Dada a função real f(x)=-x²+6x+3, determinar o conjunto f-1(8)?
- Dada a função real f3(x)=x³, qual é o conjunto f-1(8)?
- Uma sequência real é uma função real cujo domínio é o conjunto dos números naturais. Seja a sequência real definida por:
cujo gráfico é dado por
Obter os valores de f(2), f(3), f(5), f-1(8) e f-1(3/2)
- Qual dos gráficos representa uma função sobrejetora?
- Qual dos gráficos representa uma função injetora?
- Seja a função f definida sobre o conjunto A={x,y,z} com imagem em B={1,2,3}. Qual das alternativas contém os pares ordenados (x,y) de elementos em A×B que representam uma função bijetora (injetora e sobrejetora).
a. {(x,3),(y,1),(z,2)}
b. {(x,1),(y,2),(x,3),(z,1)}
c. {(y,2),(x,2),(z,3)}
d. {(x,1),(y,3),(z,2),(z,1)}
- Ao analisar a função real f definida por f(x)=x²+4x-12, podemos afirmar que f é injetora? Justifique a resposta.
Quais das funções são sobrejetoras?a. f(x)=-x+3
b. f(x)=3
c. f(x)=x³-1
d. f(x)=-x²-1
Funções Compostas- Se f(x)=3x-5, g(x)=x²+2x-3 e (gof)(x)=g(f(x)), obter (fog)(2), (gof)(-3), (gof)(x) e (fog)(x).
- Sejam as funções reais definidas por g(x)= 3x-2 e
Obter (gof)(1), (fog)(3), (fof)(2) e (gog)(-4).
- Dadas as funções f:AB e g:BC pelo diagrama
obter a função composta gof:AC.
- Sobre o conjunto A={a,b,c,d}, definimos as funçõesf={(a,d),(b,c),(c,b),(d,a)}
g={(a,b),(b,c),(c,d),(d,d)}Determinar as compostas gof e fog.
- Definidas as funções f, g e h, pelo diagrama:
determinar fog, goh, hof, gog nos pontos 1, 2 e 3.
- Dadas as funções reais f(x)=3x-1 e g(x)=x(x+2), obter gof, fog, gog e fof.
Operações com funções- Por definição (f+g)(x)=f(x)+g(x). Realizar a soma das funções f e g é o mesmo que obter os valores de f+g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa mostra a função f+g?a. {(1,7),(2,5),(6,7),(4,6)}
b. {(2,7),(4,5),(6,7),(8,6)}
c. {(1,7),(2,5),(3,7),(4,6)}
d. {(1,7),(2,5),(6,7),(8,6)}
- Por definição (f-g)(x)=f(x)-g(x). Realizar a diferença entre as funções f e g é o mesmo que obter os valores de f-g em todos os pontos do domínio comum a ambas as funções. Sejam as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f-g?a. {(0,-3),(0,1),(0,1),(0,4)}
b. {(1,3),(2,-1),(3,-1),(4,-4)}
c. {(1,3),(2,1),(3,-1),(4,4)}
d. {(1,-3),(2,1),(3,1),(4,4)}
- Por definição (f.g)(x)=f(x).g(x). Realizar o produto das funções f e g é o mesmo que obter os valores de f.g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f.g?a. {(1,7),(4,6),(9,12),(16,5)}
b. {(1,10),(2,6),(3,12),(4,5)}
c. {(1,10),(4,3),(9,12),(16,5)}
d. {(1,10),(4,3),(3,12),(4,5)}
- Por definição (f/g)(x)=f(x)/g(x). Realizar a divisão entre as funções f e g é o mesmo que obter os valores de f/g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,5),(2,3),(3,9),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f/g?a. {(1,1),(1,3/2),(1,3),(1,5)}
b. {(1,1),(2,3/2),(3,12),(4,5)}
c. {(1,1),(4,3/2),(9,12),(16,5)}
d. {(1,1),(2,3/2),(3,3),(4,5)}
- Determinar f+g, f-g, f.g e f/g, para as funções reais:f={(1,4),(2,5),(3,12),(4,2)}
g={(1,4),(2,2),(3,3),(4,6)}
Gráficos de funções- Observe os gráficos e relacione os mesmos com as respectivas funções:
a. f(x)=x³-4
b. g(x)=5
c. h(x)=2x+3
d. t(x)=x²-2
- Em cada gráfico, analise o intervalo de crescimento e de decrescimento.
a) f(x)=x³ b) g(x)=x² c) h(x)=3x-15 d) f(x)=-2x 
- Em cada gráfico, analise o intervalo de crescimento e de decrescimento.
a) f(x)=-x²+4x-4 b) g(x)=3/x c) h(x)=2 
- Analisar as funções apresentadas e identificar os seus respectivos domínios. Aqui estamos usando R[z] para a raiz quadrada de z>0.
- f(x)=4/(x-5)
- g(x)=R[x+3]
- h(x)=14x-12
- f(x)=3x+5x1/3-4
- g(x)=8x-3x²-16
- Determinar a imagem para cada função:
a) f(x)=x+1 b) g(x)=3 c) h(x)=x²+2 
- Determinar as imagens para as funções: f(x)=sen(x) e g={(-2,-2),(-1,2),(0,4),(1,1),(2,3),(3,3)}.
- Qual é a imagem da função f(x)=(x-1)(x-5) definida sobre o conjunto D={1,2,3,4,5} que é o domínio de f.
- Construir um esboço gráfico para cada função:
a. f(x)=|x-2| b. f(x)=|x|+3 c. f(x)=|x+2|-2
- Sejam as funções f(x)=2x-4 e g(x)=3x+a. Se f(1)-g(0)=6, quanto vale f(2)+5g(7)=?
a. -8 b. 65 c. 0 d. 13
- O vértice de uma função quadrática (do segundo grau) da forma f(x)=ax²+bx+c pode ser obtido por:
onde 
=b²-4ac é o discriminante da função f. Para cada uma das funções abaixo, obtenha o vértice da parábola.a. f(x)=x²-10x+21
b. g(x)=x²-2x
c. h(x)=x²-1
d. m(x)=x²+14x+49
- Os zeros de uma função quadrática f(x)=x²+bx+c são p=-7 e q=-1. Obter o vértice da parábola que representa o gráfico desta função.
- Os zeros da função quadrática f(x)=ax²+bx+c, são p=2 e q=1 e seu vértice está em (3/2,-1/4). Qual é a respectiva função?
| Tipo de função | característica deste tipo de função | Conjunto imagem | Explicação visual | Exemplo | Admite Função inversa?/ é inversível? |
|---|---|---|---|---|---|
| Funções injectoras (ou injectivas) | Cada elemento da imagem (da saída) está associado a apenas um elemento do domínio (da entrada), isto é uma relação um para um entre os elementos do domínio e daimagem. Isto é, quando no domínio então no contradomínio. A cardinalidade docontra-domínio é sempre maior ou igual à do domínio em uma função inje(c)tora. | Maior ou igual ao contradomínio (ou seja, podem haver mais elementos nocontra-domínioque no conjunto imagem da função). |  | f: N --> N dada por f(x) = 2x (é injetiva porque, sempre que tomamos dois valores diferentes de x (digamos a e b), obtemos valores diferentes para f(x) (digamos f(a)≠f(b)). Notar que esta funçãonão é sobrejetiva. | Não necessariamente, , mas sempre admite inversa à esquerda. |
| Funções sobrejetoras (ou sobrejetiva) | Todos os elementos do contra-domínio (da saída) estão associados a algum elemento do domínio (da entrada). | Igual ao conjunto contra-domínio |  | A função f:R→R definida por f(x)=6x não é sobrejetora, pois o número -1 é elemento do contradomínio R e não é imagem de qualquer elemento do domínio. | Não necessariamente, , mas sempre admite inversa à direita. |
| Funções bijetoras (ou bijetiva) | São ao mesmo tempo sobrejetoras e injetoras, isto é, todos os elementos do domínio estão associados a todos os elementos do contra-domínio de forma um para um e exclusiva. | Igual ao conjunto contra-domínio |  | função identidade | Sim, sempre; imagem (=contra-domínio, neste caso) vira domínio e vice-versa. |
Sejam f e g funções de R em R, sendo R o conjunto dos números reais, dadas por
f(x) = 2x - 3 e f(g(x)) = -4x + 1. Nestas condições, g(-1) é igual a:
a) -5
b) -4
c) 0
d) 4
e) 5
O maior valor assumido pela função y = 2 - ½ x - 2½ é:
a) 1
b) 2
c) 3
d) 4
e) 5
O gráfico da função f de R em R, dada por f(x) = ½ 1 - x½ - 2, intercepta o eixo das
abcissas nos pontos (a,b) e (c,d). Nestas condições o valor de d + c - b - a é:
a) 4
b) -4
c) 5
d) -5
e) 0
Se f (g (x) ) = 5x - 2 e f (x) = 5x + 4 , então g(x) é igual a:
a) x - 2
b) x - 6
c) x - 6/5
d) 5x - 2
e) 5x + 2
Chama-se ponto fixo de uma função f a um número x tal que f(x) = x. Se o ponto fixo da
função f(x) = mx + 5 é igual a 10, então podemos afirmar que o módulo do décuplo do ponto fixo da
função g(x) = 2x - m é igual a:
a) 5
b) 4
c) 3
d) 2
e) 1
A imagem da função f(x) = (4x + 2) / 3 é (-¥ , 5] , para todo x pertencente a R tal que:
a) x
£ 13/4
b) x
< 3/4
c) x
£ 3/4
d) x
< 17/4
e) x
< 11
Seja f : R ® R , uma função tal que f ( x ) = k.x - 1. Se f [ f ( 2 ) ] = 0 e f é estritamente
decrescente, o valor da k-ésima potência de 2 é igual aproximadamente a:
a) 0,500
b) 0,866
c) 0,125
d) 0,366
e) 0,707
Seja f(x) = ax + b; se os pares ordenados (1,5)
Î f e (2,9) Î f então podemos afirmar
que o valor do produto (a + b) (10a + 5b) é igual a:
a) 225
b) 525
c) 255
d) 100
e) 1000
A função f é tal que f(2x + 3) = 3x + 2. Nestas condições, f(3x + 2) é igual a:
a) 2x + 3
b) 3x + 2
c) (2x + 3) / 2
d) (9x + 1) /2
e) (9x - 1) / 3
Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que
a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
O conjunto imagem da função y = 1 / (x - 1) é o conjunto:
a) R - { 1 }
b) [0,2]
c) R - {0}
d) [0,2)
e) (-¥ ,2]
Dadas as proposições:
p: Existem funções que não são pares nem ímpares.
q: O gráfico de uma função par é uma curva simétrica em relação ao eixo dos y.
r: Toda função de A em B é uma relação de A em B.
s: A composição de funções é uma operação comutativa.
t: O gráfico cartesiano da função y = x / x é uma reta.
Podemos afirmar que são falsas:
a)nenhuma
b) todas
c) p,q e r
d) s e t
e) r, s e t
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente
se k for igual a:
a) -1/3
b) 1/3
c) 0
d) 1
e) -1
Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
d) 5 - 2x
e) uma função par.
Sendo f e g duas funções definidas por f(x) = 6 - 2x e g(x) = 4 -x e sabendo-se que
para " x ¹ 4 , f(x) / g(x) ³ 2, então:
a) x
³ 4
b) x
< 4
c) x
> 4
d) x = 4
e) x
£ 4
Seja a função definida por f(x) = (2x - 3) / 5x. O elemento do domínio de f que tem
-2/5 como imagem é:
a) 0
b) 2/5
c) -3
d) 3/4
e) 4/3
A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos
afirmar que f(1) é igual a:
a) 2
b) -2
c) 0
d) 3
e) -3
Se f(x) = 1 - 1/x , com x ¹ 0 , então determine o valor de
R = 96. f(2) . f(3) . f(4) . ... . f(14) . f(15) . f(16).
Resp: 6
A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos
afirmar que f(1) é igual a:
a) 2
b) -2
c) 0
d) 3
e) -3
Se f(x) = 1/[x(x+1)] com x¹ 0 e x¹ -1, então o valor de S = f(1) + f(2) + f(3) + ... + f(100)
é:
a)100
b) 101
c) 100/101
d) 101/100
e) 1
Uma função real é tal que f(x). f(y) = f(x + y) , f(1) = 3 e f(Ö 3) = 4. O valor de f(2 + Ö 3)
é:
a) 18
b) 24
*c) 36
d) 42
e) 48
Sendo f uma função definida por f(x - 1) = 2 . f(x) + f(x + 1) , tal que f(0) = 2 e
f(1) = -1 , o valor de ½ f(3) ½ é:
01) 1
02) 3
03) 16
04) 8
05) 9
Seja f uma função de N em N , tal que f(0) = -1 , f(1) = 1 e f(n-2) = f(n) . f(n-1),
se n
³ 2. O conjunto imagem de f é:
a) N
b) N - {0}
c) {-2,-1,0,1,2}
d) {-1,0,1}
e) {-1,1}
Sendo f(x) = 100x + 3 , o valor de [f(10-8) - f(103)] / (10-8 - 103) é:
a) 10000
b) 100
c) 10
d)10
-5
e) 10
-11 .
Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto (-1 , 8) pertence
ao gráfico dessa função, então:
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor máximo é 0,25
d) o seu valor mínimo é 12,5
e) o seu valor máximo é 12,5.
Que número excede o seu quadrado o máximo possível?
a) 1/2
b) 2
c) 1
d) 4
e) -1/2
A diferença entre dois números é 8. Para que o produto seja o menor possível, um
deles deve ser:
a) 16
b) 8
c) 4
d) -4
e) -16
A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:
a) 16
b) 8
c) 4
d) -4
e) -16
Se x1 e x2 são os zeros da função y = 3x2 + 4x - 2 , então o valor de 1/x1 + 1/x2 é igual
a:
a) 1/8
b) 8/3
c) 1
d) 2
e) 3
Gabarito Funções
01 D 16 D
02 B 17 A
03 A 18 6
04 C 19 A
05 A 20 C
06 A 21 C
07 E 22 E
08 A 23 E
09 D 24 B
10 A 25 E
11 C 26 A
12 D 27 C
13 A 28 E
14 D 29 D
15 C
29 – (UEFS)
28 - (INFO)
27 - (INFO)
26 - (INFO)
25 – (UCSal)
24 – (UFBA)
23 – (UCSal-95)
22 – (UEFS-95/1)
21 – (UEFS)
20 - (INFO)
19 - (INFO)
18 - (INFO)
17 - (INFO)
16 – (PUC-RS)
15 - (INFO)
14 - (INFO)
13 - (INFO)
12 - (INFO)
11 - (INFO)
10 - (INFO)
9 - (INFO)
8 - (INFO)
7 - (INFO)
6 (UEFS)
5 – (INFO)
4 – (UFBA)
3 – (UCSal)
2 – (UCSal)
1 – (UCSal)
Explicitando conjuntos
- Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir a relação R em A×B que está apresentada no gráfico.Qual resposta mostra a relação R de forma explicita?
a. R={(a,1),(b,3),(c,4),(a,3)} b. R={(1,a),(4,a),(3,b),(c,2)} c. R={(a,1),(b,3),(c,2)} d. R={(a,1),(a,4),(b,3),(c,2)} - Com a mesma relação R do exercício anterior, qual das alternativas é a relação inversa R-1?
- R-1={(a,1),(a,4),(b,3),(c,2)}
- R-1={(1,a),(4,a),(3,b),(2,c)}
- R-1={(4,a),(2,c),(3,b)}
- R-1={(1,a),(2,c)}
- Sejam os conjuntos A={a,b,c,d,e} e B={2,4,6,8,10} e a relação R, mostrada no gráfico.Quais são as formas explícitas da relação R e da relação inversa R-1?
- Sejam os conjuntos A={1,2,3} e B={1,3,4,5} de números reais e a relação definida por R={(x,y)A×B: y=2x-1}. Qual dos gráficos cartesianos abaixo, representa a relação R?
- Sejam os conjuntos A={1,3,4,5} e B={0,6,12,20} e a relação R={(x,y) em A×B: y=x(x-1)} definida sobre A×B. Escrever R de uma forma explicita e construir o gráfico cartesiano desta relação.
- Seja A={1,2,3,5,7}. Analisar o gráfico cartesiano da relação R em A×A e responder às questões pertinentes a esta relação.Qual das alternativas abaixo é verdadeira?
- (2,3)R, (5,1)R, (7,7)R
- (1,1)R, (3,5)R, (5,1)R
- (1,1)R, (5,5)R, (3,5)R
- (2,3)R, (3,5)R, (7,7)R
Dominio, contradominio, imagem, relações direta e inversa
- Para a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} definida sobre o conjunto A={1,2,3,5,7}, responda qual das alternativas abaixo representa o contradomínio da relação R. (Dica: Ver o gráfico do Exercício 6)
a. CoDom(R)={1,2,3,5,7} b. CoDom(R)={1,3,5,7} c. CoDom(R)=R d. CoDom(R)={3,5,7} - Seja a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} def. sobre A={1,2,3,5,7}. Qual alternativa representa o domínio de R. (Dica: Ver o gráfico do Exercício 6)
a. Dom(R)=R b. Dom(R)={2,5,7} c. Dom(R)={1,2,7} d. Dom(R)={1,2,3,5,7} - Para a relação R={(1,1),(2,3),(3,7),(5,1),(7,7)} def. sobre A={1,2,3,5,7}, qual das alternativas representa a imagem de R. (Dica: Ver o gráfico do Exercício 6)
a. Im(R)={1,2,3,5,7} b. Im(R)={1,3,5,7} c. Im(R)={1,3,5} d. Im(R)=R - Sejam A={2,4,6,8}, B={1,3,5,7} e a relação R em A×B apresentada pelo seu gráfico cartesiano.Identifique se cada afirmação é V (verdadeira) ou F (falsa).
a. (2,1) pertence à relação R. b. (3,2) pertence à relação R. c. (4,3) pertence à relação R. d. (5,6) pertence à relação R. e. (8,7) pertence à relação R. - Usando as informações do exercício anterior, apresente o contradomínio da relação R e a inversa da relação R, denotada por R-1.
Neste trabalho, o conjunto dos números naturais será denotado por N={1,2,3,4,5,6,7,...}. - Seja a relação R={(x,y)N×N: 2x+y=8}. Qual dos ítens representa o domínio da relação R?
a. {8} b. N c. {1,2,3} d. {2,4,6} - Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das respostas abaixo representa o contradomínio de R?
a. {1,3,5,7} b. {0,1,2,3,4,5,6,7} c. {0,2,4,6} d. N - Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das alternativas abaixo representa a imagem de R?
a. {1,3,5,7} b. {2,4,6} c. Ø d. N - Seja a relação R={(x,y) em N×N: 2x+y=8}. A relação inversa denotada por R-1 está indicada em qual das alternativas?
a. {(6,1),(4,2),(2,3)} b. Ø c. {(1,6),(2,4),(3,2)} d. N
Relações reflexivas, simétricas, transitivas e anti-simétricas
- Seja A={1,3,8} e as relações abaixo, definidas sobre A. Quais das alternativas indicam a ocorrência da propriedade reflexiva?
a. R1={(1,1),(1,3),(3,3),(3,1),(8,1)} b. R2={(1,1),(3,1),(1,8),(3,3),(8,8)} c. R3={(3,1),(3,3),(5,8),(1,1),(8,8)} d. R4={(8,8),(3,3),(1,8),(3,1),(1,1)} e. R5={(8,8),(3,3)} - Dadas as relações definidas sobre C={1,3,5}, qual delas alternativas mostra uma relação simétrica?
a. R1={(1,3),(5,3),(5,5),(3,5)} b. R2={(1,3),(3,1),(5,5),(1,5)} c. R3={(3,1),(3,3),(5,5),(5,1)} d. R4={(1,1),(3,3),(5,5)} - A relação R={(1,3),(3,3),(2,4),(3,1),(2,3),(3,2)} def. sobre A={1,2,3,4,5} é simétrica?
- Sejam as relações definidas nos conjuntos indicados. Qual delas é uma relação transitiva?
a. Ra={(2,6),(6,8),(8,2)},conjunto A={2,6,8}. b. Rb={(1,3),(3,4),(1,2)},conjunto B={1,2,3,4}. c. Rc={(1,3),(3,5),(1,5)},conjunto C={1,3,5}. d. Rd={(1,2),(2,3),(3,2)},conjunto D={1,2,3}. - Dado o conjunto A={1,3,8} e as relações sobre A listadas abaixo, indique qual alternativa mostra uma relação anti-simétrica. Justifique porque as outras relações não são anti-simétricas.
a. R1={(1,3),(3,1),(8,1)} b. R2={(1,8),(8,8),(1,3),(8,1)} c. R3={(3,3),(1,8),(8,8),(8,1)} d. R4={(8,8),(1,3),(8,1),(1,1)}
Definição de função
- Quais dos diagramas abaixo se encaixa na definição de função de A em B, onde A={a,b,c} e B={1,2,3}.
- Quais dos diagramas abaixo não representa uma função de A em B, onde A={a,b,c} e B={1,2,3}.
- Dada a função real f(x)=2x+3 definida sobre o conjunto A={1,2,3,4}, apresente o conjunto de todos os pares ordenados pertencentes à função f.
- Dada a função f:RR definida por:determinar: f(0), f(-4), f(2) e f(10).
- Qual conjunto é formado pelos valores f(0), f(-3), f(2) e f(10), se a função de R×R está definida por f(x)=x²-4x+7?
a. {67,3,4,7} b. {0,-3,2,10} c. {7,28,3,67} d. {10,2,-3,0} - Calcular os valores: f(3), f(1), f(0) e f(-10), para a função real f=f(x) definida por:
Zeros de funções
- Por definição, zero de uma função é o ponto do domínio de f onde a função se anula. Dadas as quatro funções:f(x)=3x-8, g(x)=2x+6, h(x)=x-1 e i(x)=15x-30qual dos conjuntos contém os zeros de todas as funções.
a. {-8,2,-1,-30} b. {8/3,-3,1,2} c. {-8/3,2,-1,-2} d. {2,8/3,3,30} - Se uma função do primeiro grau é da forma f(x)=ax+b tal que b=-11 e f(3)=7, obtenha o valor da constante a.
- Usando f(x)=ax+b e sabendo-se que f(-2)=8 e f(-1)=2, obter os valores de a e b.
- Obter a função f(x)=ax+b tal que f(-3)=9 e f(5)=-7. Obtenha f(1) e o zero desta função.
- Para a função real definida por f(x)=x²+2x-3, obtenha: f-1(5), f-1(0), f-1(-3) e f-1(x+3)
- Para a função real f(x)=2x+4, qual é o conjunto f-1(8)?
- Dada a função real f(x)=-x²+6x+3, determinar o conjunto f-1(8)?
- Dada a função real f3(x)=x³, qual é o conjunto f-1(8)?
- Uma sequência real é uma função real cujo domínio é o conjunto dos números naturais. Seja a sequência real definida por:cujo gráfico é dado porObter os valores de f(2), f(3), f(5), f-1(8) e f-1(3/2)
- Qual dos gráficos representa uma função sobrejetora?
- Qual dos gráficos representa uma função injetora?
- Seja a função f definida sobre o conjunto A={x,y,z} com imagem em B={1,2,3}. Qual das alternativas contém os pares ordenados (x,y) de elementos em A×B que representam uma função bijetora (injetora e sobrejetora).
a. {(x,3),(y,1),(z,2)} b. {(x,1),(y,2),(x,3),(z,1)} c. {(y,2),(x,2),(z,3)} d. {(x,1),(y,3),(z,2),(z,1)} - Ao analisar a função real f definida por f(x)=x²+4x-12, podemos afirmar que f é injetora? Justifique a resposta.
- Quais das funções são sobrejetoras?
a. f(x)=-x+3 b. f(x)=3 c. f(x)=x³-1 d. f(x)=-x²-1
Funções Compostas
- Se f(x)=3x-5, g(x)=x²+2x-3 e (gof)(x)=g(f(x)), obter (fog)(2), (gof)(-3), (gof)(x) e (fog)(x).
- Sejam as funções reais definidas por g(x)= 3x-2 eObter (gof)(1), (fog)(3), (fof)(2) e (gog)(-4).
- Dadas as funções f:AB e g:BC pelo diagramaobter a função composta gof:AC.
- Sobre o conjunto A={a,b,c,d}, definimos as funçõesf={(a,d),(b,c),(c,b),(d,a)}
g={(a,b),(b,c),(c,d),(d,d)}Determinar as compostas gof e fog. - Definidas as funções f, g e h, pelo diagrama:determinar fog, goh, hof, gog nos pontos 1, 2 e 3.
- Dadas as funções reais f(x)=3x-1 e g(x)=x(x+2), obter gof, fog, gog e fof.
Operações com funções
- Por definição (f+g)(x)=f(x)+g(x). Realizar a soma das funções f e g é o mesmo que obter os valores de f+g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa mostra a função f+g?a. {(1,7),(2,5),(6,7),(4,6)} b. {(2,7),(4,5),(6,7),(8,6)} c. {(1,7),(2,5),(3,7),(4,6)} d. {(1,7),(2,5),(6,7),(8,6)} - Por definição (f-g)(x)=f(x)-g(x). Realizar a diferença entre as funções f e g é o mesmo que obter os valores de f-g em todos os pontos do domínio comum a ambas as funções. Sejam as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f-g?a. {(0,-3),(0,1),(0,1),(0,4)} b. {(1,3),(2,-1),(3,-1),(4,-4)} c. {(1,3),(2,1),(3,-1),(4,4)} d. {(1,-3),(2,1),(3,1),(4,4)} - Por definição (f.g)(x)=f(x).g(x). Realizar o produto das funções f e g é o mesmo que obter os valores de f.g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f.g?a. {(1,7),(4,6),(9,12),(16,5)} b. {(1,10),(2,6),(3,12),(4,5)} c. {(1,10),(4,3),(9,12),(16,5)} d. {(1,10),(4,3),(3,12),(4,5)} - Por definição (f/g)(x)=f(x)/g(x). Realizar a divisão entre as funções f e g é o mesmo que obter os valores de f/g em todos os pontos do domínio comum a ambas as funções. Consideremos as funções reais:f={(1,5),(2,3),(3,9),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}Qual alternativa representa a função f/g?a. {(1,1),(1,3/2),(1,3),(1,5)} b. {(1,1),(2,3/2),(3,12),(4,5)} c. {(1,1),(4,3/2),(9,12),(16,5)} d. {(1,1),(2,3/2),(3,3),(4,5)} - Determinar f+g, f-g, f.g e f/g, para as funções reais:f={(1,4),(2,5),(3,12),(4,2)}
g={(1,4),(2,2),(3,3),(4,6)}
Gráficos de funções
- Observe os gráficos e relacione os mesmos com as respectivas funções:
a. f(x)=x³-4 b. g(x)=5 c. h(x)=2x+3 d. t(x)=x²-2 - Em cada gráfico, analise o intervalo de crescimento e de decrescimento.
a) f(x)=x³ b) g(x)=x² c) h(x)=3x-15 d) f(x)=-2x - Em cada gráfico, analise o intervalo de crescimento e de decrescimento.
a) f(x)=-x²+4x-4 b) g(x)=3/x c) h(x)=2 - Analisar as funções apresentadas e identificar os seus respectivos domínios. Aqui estamos usando R[z] para a raiz quadrada de z>0.
- f(x)=4/(x-5)
- g(x)=R[x+3]
- h(x)=14x-12
- f(x)=3x+5x1/3-4
- g(x)=8x-3x²-16
- Determinar a imagem para cada função:
a) f(x)=x+1 b) g(x)=3 c) h(x)=x²+2 - Determinar as imagens para as funções: f(x)=sen(x) e g={(-2,-2),(-1,2),(0,4),(1,1),(2,3),(3,3)}.
- Qual é a imagem da função f(x)=(x-1)(x-5) definida sobre o conjunto D={1,2,3,4,5} que é o domínio de f.
- Construir um esboço gráfico para cada função:
a. f(x)=|x-2| b. f(x)=|x|+3 c. f(x)=|x+2|-2 - Sejam as funções f(x)=2x-4 e g(x)=3x+a. Se f(1)-g(0)=6, quanto vale f(2)+5g(7)=?
a. -8 b. 65 c. 0 d. 13 - O vértice de uma função quadrática (do segundo grau) da forma f(x)=ax²+bx+c pode ser obtido por:onde=b²-4ac é o discriminante da função f. Para cada uma das funções abaixo, obtenha o vértice da parábola.
a. f(x)=x²-10x+21 b. g(x)=x²-2x c. h(x)=x²-1 d. m(x)=x²+14x+49 - Os zeros de uma função quadrática f(x)=x²+bx+c são p=-7 e q=-1. Obter o vértice da parábola que representa o gráfico desta função.
- Os zeros da função quadrática f(x)=ax²+bx+c, são p=2 e q=1 e seu vértice está em (3/2,-1/4). Qual é a respectiva função?
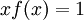
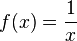
Nenhum comentário:
Postar um comentário