Aprenda Mais Sobre Funções
Clique no Link
Bons Estudos!
Função do 1º grau
Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência:
Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence ao segundo conjunto dado.
Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6} consideremos a correspondência de A em B, de tal modo que cada elemento do conjunto A se associa no conjunto B com o seu sucessor. Assim  ;
;  ;
;  . A correspondência por pares ordenados seria:
. A correspondência por pares ordenados seria:
 ;
;  ;
;  . A correspondência por pares ordenados seria:
. A correspondência por pares ordenados seria:
Assista aos vídeos:
Noções de função:
Considere os diagramas abaixo:
| 1  | 2  | |||||
| 3  | 4  | |||||
5  |
|
Analisando os diagramas acima:
O diagrama 1 não satisfaz a condição (1); os diagramas 3, 4 e 5 não satisfazem a condição (2).
Logo, somente o diagrama 2 representa uma função.
Domínio, Contradomínio e Imagem
Observe o diagrama a seguir:
 |
Chamemos esta função de f, logo o conjunto de pares ordenados serão:
f={(1,2),(2,3),(3,4)}
O conjunto X={1,2,3} denomina-se domínio da função f.
D(F)=X
O conjunto Y={1,2,3,4,5} denomina-se contradomínio da função f.
C(F)=Y
Dizemos que 2 é a imagem de 1 pela função f.
f(1)=2
Ainda, f(2)=3 e f(3)=4.
Logo o conjunto das imagens de f e dado por:
Im(f)={2,3,4}
Determinação de função:
Observe:
1) Associe cada elemento de X com o seu consecutivo:
 |
2) Associe cada elemento de X com a sua capital.
 |
3) Determine o conjunto imagem de cada função:
a) D(f) = {1,2,3}
y = f(x) = x + 1
y = f(x) = x + 1
[Sol] f(1) = 1+1 = 2
f(2) = 2+1 = 3
f(3) =3+1 = 4
f(2) = 2+1 = 3
f(3) =3+1 = 4
Logo: Im(f)={2,3,4}
b) D(f) = {1,3,5}
y = f(x) = x²
y = f(x) = x²
[Sol] f(1) = 1² = 1
f(3) = 3² = 9
f(5) = 5² = 25
f(3) = 3² = 9
f(5) = 5² = 25
Logo: Im(f)={1,9,25}
Plano cartesiano

Consideremos dois eixos x e y perpendiculares em 0, os quais determinam o plano A.
Dado um plano P qualquer, pertencente ao plano A, conduzamos por ele duas retas:
x // x' e y // y'
Denominemos P1 a interseção de x com y' e P2 a interseção de y com x'
Dado um plano P qualquer, pertencente ao plano A, conduzamos por ele duas retas:
x // x' e y // y'
Denominemos P1 a interseção de x com y' e P2 a interseção de y com x'
Nessas condições, definimos:
- Abscissa de P é um número real representado por P1
- Ordenada de P é um número real representado por P2
- A coordenada de P são números reais x' e y' , geralmente indicados na forma de par ordenado ( x' , y' )
- O eixo das abscissas é o eixo x
- O eixo das ordenadas é o eixo y
- A origem do sistema é o ponto 0
- Plano cartesiano é o plano A.
- Abscissa de P é um número real representado por P1
- Ordenada de P é um número real representado por P2
- A coordenada de P são números reais x' e y' , geralmente indicados na forma de par ordenado ( x' , y' )
- O eixo das abscissas é o eixo x
- O eixo das ordenadas é o eixo y
- A origem do sistema é o ponto 0
- Plano cartesiano é o plano A.
Depois desta revisão, vamos finalmente ver a Função do 1º grau!
Exemplo:
Numa loja, o salário fixo mensal de um vendedor é 500 reais. Além disso, ele recebe de comissão 50 reais por produto vendido.
a) Escreva uma equação que expresse o ganho mensal y desse vendedor, em função do número x de produto vendido.
[Sol] y=salário fixo + comissão
y=500 + 50x
y=500 + 50x
b) Quanto ele ganhará no final do mês se vendeu 4 produtos?
[Sol] y=500+50x , onde x=4
y=500+50.4 = 500+200 = 700
y=500+50.4 = 500+200 = 700
c) Quantos produtos ele vendeu se no final do mês recebeu 1000 reais?
[Sol] y=500+50x , onde y=1000
1000=500+50x » 50x=1000-500 » 50x=500 » x=10
1000=500+50x » 50x=1000-500 » 50x=500 » x=10
A relação assim definida por uma equação do 1º grau é denominada função do 1º grau, sendo dada por:
y=f(x)=ax+b com  , ,  e e  |
Gráfico da função do 1º grau:
O gráfico de uma função do 1º grau de R em R é uma reta. |
Exemplo:
1) Construa o gráfico da função determinada por f(x)=x+1:
[Sol] Atribuindo valores reais para x, obtemos seus valores correspondentes para y.
| O conjunto dos pares ordenados determinados é f={(-2,-1),(-1,0),(0,1),(1,2),(2,3)}
|
2) Construa o gráfico da função determinada por f(x)=-x+1.
[Sol] Atribuindo valores reais para x, obtemos seus valores correspondentes para y.
| O conjunto dos pares ordenados determinados é f={(-2,3),(-1,2),(0,1),(1,0),(2,-1)}
|
Gráficos crescente e decrescente respectivamente:
y = x+1 ( a> 0 ) ; onde a = 1 |
 |
Função crescente |
| |
| y = -x+1 ( a<0 ); onde a=-1 |
 |
Função decrescente |
Raiz ou zero da função do 1º grau:
|
1) Considere a função dada pela equação y=x+1, determine a raiz desta função.
[Sol] Basta determinar o valor de x para termos y=0
x+1=0 » x=-1
Dizemos que -1 é a raiz ou zero da função.
 |
Note que o gráfico da função y=x+1, interceptará (cortará) o eixo x em -1, que é a raiz da função.
2) Determine a raiz da função y=-x+1 e esboce o gráfico.
[Sol] Fazendo y=0, temos:
0 = -x+1 » x = 1
0 = -x+1 » x = 1
Gráfico:
 |
Note que o gráfico da função y=-x+1, interceptará (cortará) o eixo x em 1, que é a raiz da função.
Sinal de uma função de 1º grau:
Observe os gráficos:
 |  |
a>0 | a<0 |
Note que para x=-b/a, f(x)=0 (zero da função). Para x>-b/a, f(x) tem o mesmo sinal de a. Para x<-b/a, f(x) tem o sinal contrário ao de a.
Exemplos:
1) Determine o intervalo das seguintes funções para que f(x)>0 e f(x)<0.
a) y=f(x)=x+1
[Sol] x+1>0 » x>-1
Logo, f(x) será maior que 0 quando x>-1
Logo, f(x) será maior que 0 quando x>-1
x+1<0 » x<-1
Logo, f(x) será menor que 0 quando x<-1
Logo, f(x) será menor que 0 quando x<-1
b) y=f(x)=-x+1
[Sol]* -x+1>0 » -x>-1 » x<1
Logo, f(x) será maior que 0 quando x<1
Logo, f(x) será maior que 0 quando x<1
-x+1<0 » -x<-1 » x>1
Logo, f(x) será menor que 0 quando x>1
(*ao multiplicar por -1, inverte-se o sinal da desigualdade)
Logo, f(x) será menor que 0 quando x>1
(*ao multiplicar por -1, inverte-se o sinal da desigualdade)
Acompanhe a seção de Exercícios:
Lista de Exercícios – Função do 1º Grau
|
2- Obtenha a lei da função do 1º grau sendo dado:
a) f(-1) = 2 e f(2) = -1.
a) f(-1) = 2 e f(2) = -1.
b) f(-1) = 0 e f(3)=2
3-Faça o estudo do sinal das funções do 1º grau:
a) y = 3x – 2
b) y = –2x + 1
4- Uma escola de natação cobra de seus alunos uma matrícula de R$ 80,00, mais uma mensalidade de R$ 50,00. Nestas condições, pode-se afirmar que a função que representa os gastos de um aluno em relação aos meses de aula e o valor gasto por um aluno que nos seis primeiros meses de aula será:
a) f(x) = 80,00.x + 50,00 e R$ 530,00
b) f(x) = 50,00.x + 80,00 e R$ 380,00
c) f(x) = 80,00.x + 50,00 e R$ 380,00
d) f(x) = 50,00.x + 80,00 e R$ 530,00
e) f(x) = 50,00.x + 30,00 e R$ 380,00
5- Construa o gráfico das funções de 1º grau abaixo:
a) y = 2x-6 b) y = -2x-3 c) y = 3x+4
6- Sendo f(x) = -2x+6 e g(x) = 6x-2, determine f(g(x)) e g(f(x)).
7- (PRISE 98) Um marreteiro compra diariamente objetos por R$ 3,00 e os vende por R$ 5,00, gastando R$ 100,00 com transporte. Se x é a quantidade vendida e y o lucro diário do marreteiro, então:
a) Y = 100x b) Y = 5x -100 c) Y = 3x -100 d) Y = 2x -100
8- Para resolver problemas de computador, foram contatados os serviços de um técnico em computação. Em seus honorários, o técnico cobra R$ 20,00 a hora trabalhada, acrescida da taxa de visita de R$ 30,00. Sabe-se que, para resolver o problema, o técnico trabalhou x horas e recebeu a quantia R(x). Então:
a) R(x) = 30x + 20 b) R(x) = 20x + 30 c) R(x) = 10x
d) R(x) = 30x – 20
9- (UEPA) Um pequeno comerciante investiu R$ 300,00 na produção de bandeiras do seu time favorito, para venda em um estádio de futebol. Foram vendidas x bandeiras ao preço de R$ 8,00 cada uma. Então o lucro L(x) obtido na venda de x bandeiras é dado por:
a) L(x) = 300 - 8x b) L(x) = 8x + 300 c) L(x) = 8x - 300 d) L(x) = 8x e) L(x) = - 8x - 300
10- O custo total de produção de um determinado produto é representado pela função C(x) = x + 20, em que C é o custo ( em reais ) e x é o número de unidades produzidas. Determine:
a) O custo de fabricação de 10 unidades
b) Quantas unidades devem ser produzidas para que o custo seja de R$ 3.600,00
c) O gráfico que representa essa função.
11- Uma loja no centro de São Miguel aluga microcomputadores para usuários que desejam navegar pela internet. Para utilizar esse serviço, o usuário paga uma taxa de R$ 2,00 acrescida de R$ 3,00 por hora de utilização da maquina. O gráfico que melhor representa o preço desse serviço é:
12- Determine a lei da função do 1º grau cujo gráfico está representado abaixo:
13- Determine o domínio e a imagem da função representada no gráfico abaixo:
Questões:
01. (UNIFOR) A função f, do 1° grau, é definida por f(x) = 3x + k. O valor de k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é:
a) 1
b) 2
c) 3
d) 4
e) 5
02. (EDSON QUEIROZ - CE) O gráfico abaixo representa a função de ℝ em ℝ dada por f(x) = ax + b (a, b Îℝ). De acordo com o gráfico conclui-se que:
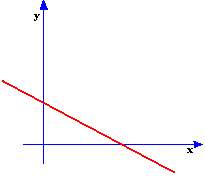
a) a < 0 e b >0
b) a < 0 e b < 0
c) a > 0 e b > 0
d) a > 0 e b < 0
e) a > o e b = 0
Resolva, em R, as inequações de 03 a 05
03. 2x - 10 < 4
04. -3x + 5 ³ 2
05. -(x - 2) ³ 2 - x
Resolva, em R, as inequações de 06 a 08
06. x - 3 ³ 3 + x
07. -x + 1 £ x + 1
08. -x - 4 > -(4 -x)
09. (MACK) Em R, o produto das soluções da inequação 2x - 3 £ 3 é:
a) maior que 8
b) 6
c) 2
d) 1
e) 0
10. (UNICAMP) Numa escola é adotado o seguinte critério: a nota da primeira prova é multiplicada por 1, a nota da segunda prova é multiplicada por 2 e anota da terceira prova é multiplicada por 3. Os resultados após somados, são divididos por 6. Se a média obtida por esse critério for maior ou igual a 6,5 o aluno é dispensado das atividades de recuperação. Suponha que um aluno tenha tirado 6,3 na primeira prova e 4,5 na segunda prova. Quanto precisará tirar na terceira prova para ser dispensado da recuperação?
Resolução:
01. E
02. A
03. V = (x Î R| x < 7)
04. V = (x Î R| x £ 1)
05. V = R
06. V = f
07. V = R
08. V = R*
09. E
10. No mínimo 7,9
a) 1
b) 2
c) 3
d) 4
e) 5
02. (EDSON QUEIROZ - CE) O gráfico abaixo representa a função de ℝ em ℝ dada por f(x) = ax + b (a, b Îℝ). De acordo com o gráfico conclui-se que:

a) a < 0 e b >0
b) a < 0 e b < 0
c) a > 0 e b > 0
d) a > 0 e b < 0
e) a > o e b = 0
Resolva, em R, as inequações de 03 a 05
03. 2x - 10 < 4
04. -3x + 5 ³ 2
05. -(x - 2) ³ 2 - x
Resolva, em R, as inequações de 06 a 08
06. x - 3 ³ 3 + x
07. -x + 1 £ x + 1
08. -x - 4 > -(4 -x)
09. (MACK) Em R, o produto das soluções da inequação 2x - 3 £ 3 é:
a) maior que 8
b) 6
c) 2
d) 1
e) 0
10.
Resolução:
01. E
02. A
03. V = (x Î R| x < 7)
04. V = (x Î R| x £ 1)
05. V = R
06. V = f
07. V = R
08. V = R*
09. E
10. No mínimo 7,9
1) O domínio da função  é
é
(A) 
(B) 
(C) 
(D) 
(E) 
2) Se  , então
, então  é igual a:
é igual a:
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
(B) 2
(C) 3
(D) 4
(E) 5
3) Se a função  é tal que
é tal que  então
então  é
é
(A) 
(B) 
(C) 
(D) 
(E) 
4) Na equação  fizemos
fizemos  , então o valor de
, então o valor de  é
é
(A) 
(B) 
(C) 
(D) 
(E) 
5) (UFRGS) - A solução da equação  é também solução da equação
é também solução da equação  . Logo o valor de
. Logo o valor de  é
é
(A) 
(B) 
(C) 
(D) 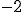
(E) 
6) Sejam  e
e  funções definidas em
funções definidas em  por
por  e
e  . O valor de
. O valor de  é
é
(A) -1
(B) 1
(C) 2
(D) 3
(E) 4
(B) 1
(C) 2
(D) 3
(E) 4
7) Considere a função  , de domínio
, de domínio  , definida por
, definida por  e
e  . O valor de
. O valor de  é
é
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
(B) 1
(C) 2
(D) 3
(E) 4
| GABARITO | ||
| 01-D | 04-C | 07-C |
| 02-D | 05-A | |
| 03-C | 06-E | |
| RESOLUÇÃO | ||
Referências:
http://www.google.com.br/search?q=exercicios+fun%C3%A7%C3%A3o+primeiro+grau&hl=pt-BR&biw=1352&bih=559&prmd=ivns&ei=mezcTYjMC4K3twej6-mgDw&start=20&sa=N
http://www.exatas.mat.br/funcao1.htm
http://www.somatematica.com.br/emedio/funcao1/funcao1_3.php
http://www.google.com.br/url?sa=t&source=web&cd=1&ved=0CBwQFjAA&url=http%3A%2F%2Fwww.supletivounicanto.com.br%2Fdocs%2Fmatematica%2Ffuncao_1_grau.pdf&ei=k-vcTdhTyaO2B_DcubYP&usg=AFQjCNFhaZVVxR8rwhBPV3WNMWHgBJvE4g&sig2=OLhWbulhf6zYiewLdhAPmg
http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/funcao-polinomial-do-primeiro-grau
http://pessoal.sercomtel.com.br/matematica/medio/funcoes/funcoes-a.htm
http://jonasportal.blogspot.com/2010/05/lista-de-exercicios-funcao-do-1-grau.html
http://br.answers.yahoo.com/question/index?qid=20071124105334AA8jk0e
http://www.google.com.br/url?sa=t&source=web&cd=9&ved=0CFcQFjAI&url=http%3A%2F%2Fwww.diaadiaeducacao.pr.gov.br%2Fportals%2Froteiropedagogico%2Frecursometod%2F7257_Atividades_utilizando_o_zgrpher.doc&ei=k-vcTdhTyaO2B_DcubYP&usg=AFQjCNEbqbGVB2uMB_GWIIkBHgk9nZYroQ&sig2=tF9X_qkoo5Lf4RKrY0BRCg
http://www.matematica.tv/estudo_matematica_online/funcoes/funcao_primeiro_grau/funcao_primeiro_grau_05_01.php
http://www.matematica.tv/estudo_matematica_online/funcoes/funcao_primeiro_grau/funcao_primeiro_grau_05_01.php





Doidao seu blog.
ResponderExcluir