Equações do 2º grau
Em matemática, uma equação quadrática ou equação do segundo grau é uma equação polinomial de grau dois. A forma geral deste tipo de equação é:
Assista aos vídeos:
Fórmula
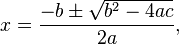
Demonstração
Se  então:
então:
Logo, tem-se, por definição de módulo, que:
Portanto,
 então:
então: |
Se  | Se  |
|---|---|
 |  |
 Forma fatorada da equação quadráticaO termo
|
Resolução das equações incompletas
c=0
É uma equação no formato ax2 + bx = 0. A solução é feita da seguinte forma: . Portanto, x = 0 ou
. Portanto, x = 0 ou  . Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).
. Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).b=0
É uma equação no formato ax2 + c = 0. A resolução é feita deste modo: . Por isso,
. Por isso,  , ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
, ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0
f) x² - 10x + 25 = 0
g) x² - x - 20 = 0
h) x² - 3x -4 = 0
i) x² - 8x + 7 = 0
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)

 1) O triplo do quadrado do número de filhos de Pedro é igual a 63 menos 12 vezes o número de filhos. Quantos filhos Pedro tem?
1) O triplo do quadrado do número de filhos de Pedro é igual a 63 menos 12 vezes o número de filhos. Quantos filhos Pedro tem?  2) Uma tela retangular com área de 9600cm2 tem de largura uma vez e meia a sua altura. Quais são as dimensões desta tela?
2) Uma tela retangular com área de 9600cm2 tem de largura uma vez e meia a sua altura. Quais são as dimensões desta tela?  3) O quadrado da minha idade menos a idade que eu tinha 20 anos atrás e igual a 2000. Quantos anos eu tenho agora?
3) O quadrado da minha idade menos a idade que eu tinha 20 anos atrás e igual a 2000. Quantos anos eu tenho agora?  4) Comprei 4 lanches a um certo valor unitário. De outro tipo de lanche, com o mesmo preço unitário, a quantidade comprada foi igual ao valor unitário de cada lanche. Paguei com duas notas de cem reais e recebi R$ 8,00 de troco. Qual o preço unitário de cada produto?
4) Comprei 4 lanches a um certo valor unitário. De outro tipo de lanche, com o mesmo preço unitário, a quantidade comprada foi igual ao valor unitário de cada lanche. Paguei com duas notas de cem reais e recebi R$ 8,00 de troco. Qual o preço unitário de cada produto?  5) O produto da idade de Pedro pela idade de Paulo é igual a 374. Pedro é 5 anos mais velho que Paulo. Quantos anos tem cada um deles?
5) O produto da idade de Pedro pela idade de Paulo é igual a 374. Pedro é 5 anos mais velho que Paulo. Quantos anos tem cada um deles?  6) Há dois números cujo triplo do quadrado é a igual 15 vezes estes números. Quais números são estes?
6) Há dois números cujo triplo do quadrado é a igual 15 vezes estes números. Quais números são estes?  7) Quais são as raízes da equação x2 - 14x + 48 = 0?
7) Quais são as raízes da equação x2 - 14x + 48 = 0?  8) O dobro do quadrado da nota final de Pedrinho é zero. Qual é a sua nota final?
8) O dobro do quadrado da nota final de Pedrinho é zero. Qual é a sua nota final?  9) Solucione a equação biquadrada: -x4 + 113x2 - 3136 = 0.
9) Solucione a equação biquadrada: -x4 + 113x2 - 3136 = 0.  10) Encontre as raízes da equação biquadrada: x4 - 20x2 - 576 = 0.
10) Encontre as raízes da equação biquadrada: x4 - 20x2 - 576 = 0.Exercícios de Equações de 2º Grau

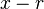


![ax^2+bx+c = a \left( x - \frac{-b + \sqrt {b^2-4ac}}{2a} \right) \left( x - \frac{-b - \sqrt {b^2-4ac}}{2a} \right) = a \left [(x - r_1)(x - r_2)\right ].](http://upload.wikimedia.org/math/7/a/0/7a02741b078e8e604d8b697b6bd7b2f6.png)
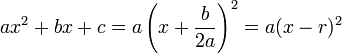




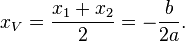
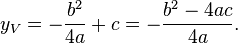




 , verificam-se as seguintes relações entre as raízes:
, verificam-se as seguintes relações entre as raízes:












Nenhum comentário:
Postar um comentário