O que é? Por que existe?

Descubra agora!

Bons Estudos!

Teorema do confronto (Sanduíche)

O chamado teorema do confronto estabelece a existência do limite de uma sequência/sucessão numérica ou função real contanto que esteja limitada entre duas sequências/sucessões ou funções convergentes para o mesmo limite.
Este teorema também é chamado de teorema do/da sanduíche , porque a sequência ou função se comporta como uma fatia de carne ensanduichada entre dois pedaços de pão.

Assista ao vídeo:

Teorema do confronto para sequências (Teorema das sucessões enquadradas)

Sejam $a_n\,$ , $b_n\,$ e $c_n\,$ sequências de números reais tais que:

$\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=L\,$

$a_n\leq b_n\leq c_n\,$

Então, $b_n\,$ é uma sequência convergente e ainda:

$\lim_{n\to\infty}b_n=L\,$

Teorema do confronto para funções (Teorema das funções enquadradas)

Sejam 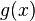$f(x)\,$ , $g(x)\,$ e $h(x)\,$ funções reais definidas em um domínio $D\subseteq\mathbb{R}\,$ e seja $a\,$ um ponto (finito ou não) deste domínio, tais que:

$\lim_{x\to a}f(x)=\lim_{x\to a}h(x)=L\,$

$f(x)\leq g(x)\leq h(x)\,$

Então existe o limite:

$\lim_{x\to a}g(x)=L\,$

Exemplo (com 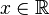$x\in\mathbb{R}$ )

Gráfico alusivo ao teorema do confronto.

Considere os gráficos à direita das funções $\frac{1}{x^2}$ (azul escuro), $\frac{\sin x}{x^2}$ (cinzento tracejado) e $-\frac{1}{x^2}$ (azul ciano).
Quando x tende para infinito (positivo) a função $\frac{\sin x}{x^2}$ fica "ensanduichada" pelas outras duas funções.

Este comportamento traduz-se analiticamente por:

$\lim_{x\to +\infty}\frac{1}{x^2}=\lim_{x\to +\infty} -\frac{1}{x^2}=0\,$

E como:

$-\frac{1}{x^2}\leq \frac{\sin x}{x^2}\leq \frac{1}{x^2}\,$ ,

Conclui-se que:

$\lim_{x\to +\infty}\frac{\sin x}{x^2}=0\,$

O resultado é análogo para as sucessões correspondentes às funções dadas, visto que a única diferença será o domínio da variável x (nesse caso, $x\in\mathbb{N}$ ).

Uma Curiosidade: Teorema do Sanduíhe

Teorema do confronto (Sanduíche)

Teorema do confronto para sequências (Teorema das sucessões enquadradas)

Teorema do confronto para funções (Teorema das funções enquadradas)

Exemplo (com $x\in\mathbb{R}$ )

Nenhum comentário:

Postar um comentário

Uma Curiosidade: Teorema do Sanduíhe

Teorema do confronto (Sanduíche)

Teorema do confronto para sequências (Teorema das sucessões enquadradas)

Teorema do confronto para funções (Teorema das funções enquadradas)

Exemplo (com )

Nenhum comentário:

Postar um comentário

Exemplo (com $x\in\mathbb{R}$ )