Prof.: Marcos Vilela Garcia: Polígonos

Propriedades e pontos notáveis nos polígonos.

Exercícios de de Vestibular e vídeo-aulas no final.

Bons Estudos!

Exercícios:

http://antoniorobertoandrade.com/teste4.pdf

Poli: Muitos; vários.

Gonos: Ângulos

Figura geométrica plana limitada por linhas poligonais

Linhas poligonais e polígonos

Linha poligonal é uma sucessão de segmentos consecutivos e não colineares, dois a dois. Classificam-se em:

Linhas poligonais e polígonos

Linha poligonal é uma sucessão de segmentos consecutivos e não-colineares, dois a dois. Classificam-se em:

Linha poligonal aberta simples

Linha poligonal aberta não-simples

Polígono é uma superfície plana limitada por linhas rectas (lados). Um polígono divide o plano em que se encontra em duas regiões (a interior e a exterior), sem pontos comuns. Um polígono estrelado é uma linha poligonal fechada não-simples com propriedades especiais.

Elementos de um polígono

Um polígono possui os seguintes elementos:

— Lados: Cada um dos segmentos de reta que une vértices consecutivos:

, ,,,.

— Vértices: Ponto de encontro de dois lados consecutivos:

 $A$ ,  $B$ ,  $C$ ,  $D$ ,  $E$ .

— Diagonais: Segmentos que unem dois vértices não consecutivos:

$\overline{A C}\$ , $\overline{A D}\$ , $\overline{B D}\$ , $\overline{B E}\$ , $\overline{C E}\$ .

— Ângulos internos: Ângulos formados por dois lados consecutivos:

,,,,

— Ângulos externos: Ângulos formados por um lado e pelo prolongamento do lado a ele consecutivo:

,,,,.

Classificação dos polígonos quanto ao número de lados

Número de lados	Polígono
1	não existe
2	não existe
3	triângulo
4	quadrilátero
5	pentágono
6	hexágono
7	heptágono
8	octágono
9	eneágono
10	decágono
11	undecágono
12	dodecágono
13	tridecágono
14	tetradecágono
15	pentadecágono
16	hexadecágono
17	heptadecágono
18	octodecágono
19	eneadecágono
20	icoságono
25	pentacoságono
30	triacontágono
40	tetracontágono
50	pentacontágono
60	hexacontágono
70	heptacontágono
80	octacontágono
90	eneacontágono
100	hectágono
1000	quilógono
1.000.000	megágono
10⁹	gigágono
10¹⁰⁰	googólgono

Soma dos Ângulos Internos e Externos de um Polígono Convexo

Em um polígono, quanto maior o número de lados, maior a medida dos ângulos internos.
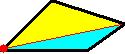
Considerando as diagonais traçadas por apenas um dos vértices de um polígono, é possível perceber que elas formam triângulos. Conforme aumentamos os lados de um polígono, a quantidade de triângulos aumenta, veja:

Em um quadrilátero conseguimos formar 2 triângulos.

Considerando que em cada triângulo a soma dos ângulos internos iguais é igual a 180°, então a soma dos ângulos internos de qualquer quadrilátero será 2 * 180º = 360º.

Em um polígono de cinco lados (pentágono) formamos 3 triângulos.

Dessa forma, temos que a soma dos ângulos internos de um pentágono é 180º * 3 = 540º

Em um polígono de seis lados (hexágono) formamos 4 triângulos.

Portanto, a soma dos ângulos internos é dada por 4 * 180º = 720º.

Percebemos que a diferença do número de triângulos formados e o número de lados dos polígonos é sempre 2, então concluímos que:

n = 3 ; Si = (3 – 2) * 180º = 1 * 180° = 180°

n = 4 ; Si = (4 – 2) * 180° = 2 * 180° = 360°

n = 5 ; Si = (5 – 2) * 180° = 3 * 180° = 540°

n = 6 ; Si = (6 – 2) * 180° = 4 * 180° = 720°

n = n ; Si = (n – 2) * 180°

Portanto, a soma dos ângulos internos de qualquer polígono será calculada através da expressão:

Si = (n – 2) * 180°

Caso queira calcular o valor de cada ângulo interno, basta dividir a soma dos ângulos internos pelo número de lados do polígono.

ai = Si / n

Soma dos ângulos externos de um polígono regular

A soma dos ângulos externos de qualquer polígono convexo, independentemente da quantidade de lados, é igual a 360°.

Obs.: A soma de um ângulo interno com o seu respectivo externo é igual a 180º, isto é, eles são suplementares.

Exemplo 1
Qual é a soma dos ângulos internos de um heptágono regular?

O heptágono possui 7 lados.
S = (n – 2) * 180º
S = (7 – 2) * 180º
S = 5 * 180º
S = 900º
A soma dos ângulos internos de um heptágono é 900º.

Exemplo 2
Qual a soma dos ângulos internos de um icoságono (20 lados)?

Aplicando a fórmula:
S = (n – 2) * 180º
S = (20 – 2) * 180º
S = 18 * 180º
S = 3240º
A soma dos ângulos internos de um icoságono é 3240º.

Podemos utilizar a fórmula da soma dos ângulos internos para calcular o número de lados de qualquer polígono, desde que a soma dos ângulos internos seja dada.

Exemplo 3
Quantos lados possui um polígono cuja soma dos ângulos internos é igual a 2340º?

S = (n – 2) * 180º
2340º = (n – 2) * 180º
2340º = 180n – 360º
2340 + 360 = 180n
2700 = 180n
180n = 2700
n = 2700/180
n = 15

O polígono possui 15 lados.

A soma dos ângulos externos de qualquer polígono regular é 360º.
Para calcular a medida do ângulo externo de um polígono é preciso dividir 360º pelo número de lados da figura poligonal.

Exemplo 4
Quanto mede o ângulo externo do hexágono?

O hexágono possui seis lados, então:

ai = 360º / 6
ai = 60º

Cada ângulo externo de um hexágono mede 60º.

Semelhança de Polígonos

Polígonos Semelhantes

Considere os polígonos ABCD e A'B'C'D', nas figuras:

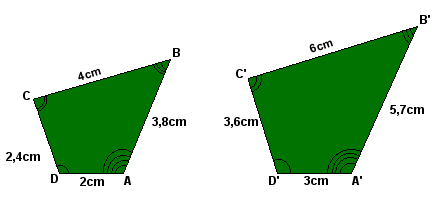
Observe que:

os ângulos correspondentes são congruentes:
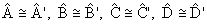
os lados correspondentes (ou homólogos) são proporcionais:

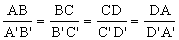
                                            ou

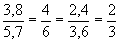
Podemos concluir que os polígonos ABCD e A'B'C'D' são semelhantes e indicamos:
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")

Ou seja:

Dois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais.

A razão entre dois lados correspondentes em polígonos semelhante denomina-se razão de semelhança, ou seja:

A razão de semelhança dos polígonos considerados é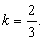

Obs: A definição de polígonos semelhantes só é válida quando ambas as condições são satisfeitas: Ângulos correspondentes congruentes e lados correspondentes proporcionais. Apenas uma das condições não é suficiente para indicar a semelhança entre polígonos.

Videos: