Concurso Fcc Parte I
2) Um grande depósito foi esvaziado a um terço da sua capacidade e mais tarde, do que sobrou foram retirados três quartos. Sabe-se que o reservatório ainda ficou com vinte mil litros de água. Qual é a capacidade total deste reservatório? 3) Se eu conseguir reduzir do valor de um produto, um quinto deste preço à vista e pagar R$ 128,00 por quatro das nove parcelas. Qual é o preço total do produto sem este desconto? 4) Dos frascos de xampu utilizados mensalmente por uma família, a mãe consome 7/9 de um frasco, a filha caçula consome 1/3 de um frasco e a mais velha consome 3/5 de um frasco, sendo que do total de mililitros ainda sobram 260 ml não consumidos. Visto que elas utilizam a menor quantidade necessária de frascos, qual é a capacidade em mililitros de cada frasco de xampu? 5) Meus dois sobrinhos me visitaram neste final de semana e lhes dei 4/5 dos doces que eu possuía em casa. Um ganhou 10 doces e outro ganhou 7/12 dos doces que eu dei. Quantos doces eu deixei de dar? 6) Um assentador de pisos consegue assentar todos os pisos de um salão em 24 horas. Um outro assentador consegue fazer o mesmo trabalho em 21 horas. Trabalhando juntos, conseguem realizar tal trabalho em quantas horas? 7) Para comprar um certo brinquedo, da quantia necessária João possui um terço e Maria possui um quarto. Dona Lurdes, a mãe deles, prometeu completar com os R$ 125,00 que faltam para eles completarem o valor. Quanto custa tal brinquedo? 8) Para transportar uma determinada carga, um caminhão A precisa de quatro viagens e um caminhão B precisa de cinco viagens. Trabalhando em conjunto com um caminhão C, eles conseguem transportar a carga em apenas duas viagens. Quantas viagens o caminhão C precisaria para transportar esta carga sozinho? 9) Um feirante vendeu metade das trezentas dúzias de laranjas que comprou, a R$ 2,00 a dúzia. Dois terços da outra metade vendeu a R$ 1,50 a dúzia e o restante vendeu a R$ 1,00 a dúzia. Qual é a fração das dúzias correspondentes a cada valor de venda e quanto o vendedor faturou na venda? Resolução:
Do total de figurinhas que eu possuía,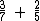 
já não possuo mais, ou seja, estou sem 
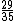delas, como demonstrado abaixo:
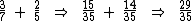
1 representa a fração total das figurinhas e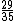 é a fração que não está mais comigo. Subtraindo um valor do outro temos:
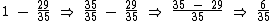
Logo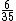
representa a parte que ficou comigo.
Se soubéssemos o total de figurinhas e o multiplicássemos por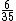, naturalmente iríamos obter 72, então se dividirmos 72 por 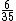iremos obter a quantidade total de figurinhas:
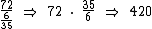
Se a quantidade total de figurinhas é igual a 420, então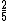
disto será:
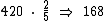
Então:
Foram dadas 168 figurinhas ao meu irmão.
1 representa a fração total das figurinhas e
Logo
Se soubéssemos o total de figurinhas e o multiplicássemos por
Se a quantidade total de figurinhas é igual a 420, então
Então:
Foram dadas 168 figurinhas ao meu irmão.2) Um grande depósito foi esvaziado a um terço da sua capacidade e mais tarde, do que sobrou foram retirados três quartos. Sabe-se que o reservatório ainda ficou com vinte mil litros de água. Qual é a capacidade total deste reservatório? Primeiramente o reservatório foi deixado com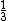 
da sua capacidade e depois reduziu-se este volume em 
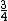do que havia restado, podemos então montar a seguinte sentença matemática:
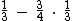
Que pode ser resumida a:
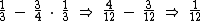
Se multiplicarmos a capacidade total do reservatório por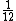
, iremos obter os 20000 litros que restam nele, obviamente realizando a operação inversa, se dividirmos os 20000 por 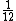iremos obter a capacidade total do depósito:
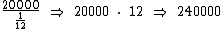
Portanto:
A capacidade total deste reservatório é de 240 mil litros.
Que pode ser resumida a:
Se multiplicarmos a capacidade total do reservatório por
Portanto:
A capacidade total deste reservatório é de 240 mil litros.3) Se eu conseguir reduzir do valor de um produto, um quinto deste preço à vista e pagar R$ 128,00 por quatro das nove parcelas. Qual é o preço total do produto sem este desconto? Se de 1 que representa a fração total do preço do produto, subtrairmos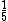 
do mesmo ficaremos apenas com 
:
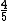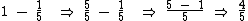
As quatro das nove parcelas, equivalem a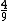
dos :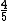
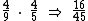
Ou seja, os R$ 128,00 equivalem a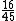
do preço total sem o desconto. Fazendo a operação inversa, se dividirmos esta quantia por esta fração, iremos obter o preço total do produto sem o desconto:
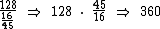
Temos então que:
O preço total do produto sem este desconto é de R$ 360,00.
As quatro das nove parcelas, equivalem a
Ou seja, os R$ 128,00 equivalem a
Temos então que:
O preço total do produto sem este desconto é de R$ 360,00.4) Dos frascos de xampu utilizados mensalmente por uma família, a mãe consome 7/9 de um frasco, a filha caçula consome 1/3 de um frasco e a mais velha consome 3/5 de um frasco, sendo que do total de mililitros ainda sobram 260 ml não consumidos. Visto que elas utilizam a menor quantidade necessária de frascos, qual é a capacidade em mililitros de cada frasco de xampu? Primeiramente devemos somar as três frações para obtermos a fração de frascos consumida por mês:
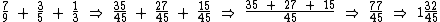
Ou seja, por mês é gasto um frasco inteiro, mais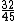
de outro frasco. Subtraindo esta fração de 1 (um frasco inteiro), teremos a fração que sobrou no frasco:
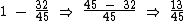
Dividindo os 260 ml por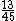
iremos obter o volume total de xampu de cada frasco:
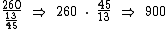
Logo, mensalmente elas utilizam 2 frascos de 900 ml, sendo que do volume total 1800 ml, ainda restam 260 ml não utilizados. Se cada uma utilizasse um frasco à parte, utilizariam 3 frascos, o que seria mais que o mínimo necessário.
A capacidade de cada frasco de xampu é de 900 ml.
Ou seja, por mês é gasto um frasco inteiro, mais
Dividindo os 260 ml por
Logo, mensalmente elas utilizam 2 frascos de 900 ml, sendo que do volume total 1800 ml, ainda restam 260 ml não utilizados. Se cada uma utilizasse um frasco à parte, utilizariam 3 frascos, o que seria mais que o mínimo necessário.
A capacidade de cada frasco de xampu é de 900 ml.5) Meus dois sobrinhos me visitaram neste final de semana e lhes dei 4/5 dos doces que eu possuía em casa. Um ganhou 10 doces e outro ganhou 7/12 dos doces que eu dei. Quantos doces eu deixei de dar? Se um dos sobrinhos ganhou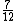 
dos doces que eu dei, o outro ganhou 
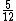deles:
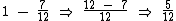
Como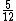 equivale a 10 doces, dividindo 10 por 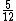teremos o total dado de doces:
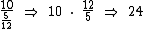
Se eu dei 24 doces, correspondentes a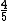 dos doces que eu possuía, então originalmente eu tinha 30 doces conforme calculado abaixo:
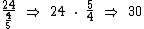
Ora, se dos 30 doces que eu possuía eu dei 24, obviamente fiquei com 6:
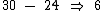
Assim sendo:
Eu deixei de dar 6 doces.
Como
Se eu dei 24 doces, correspondentes a
Ora, se dos 30 doces que eu possuía eu dei 24, obviamente fiquei com 6:
Assim sendo:
Eu deixei de dar 6 doces.6) Um assentador de pisos consegue assentar todos os pisos de um salão em 24 horas. Um outro assentador consegue fazer o mesmo trabalho em 21 horas. Trabalhando juntos, conseguem realizar tal trabalho em quantas horas? Sabemos que um dos assentadores consegue assentar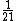 
do salão por hora, ao passo que o outro consegue assentar apenas 
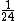neste mesmo período.
Trabalhando em conjunto, eles conseguem assentar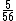
do salão por hora, que corresponde à soma destas duas frações:
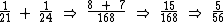
Em uma hora eles conseguem assentar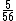 do salão, basta dividirmos 1 (o salão todo) por esta fração para encontrarmos a resposta desejada:
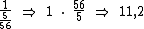
11,2 horas equivalem a 11 horas e 12 minutos, as 11 horas correspondem à parte inteira e os 12 minutos à parte fracionária multiplicada por 60, já que temos 60 minutos em uma hora.
Então:
Trabalhando juntos, os assentadores conseguem realizar tal trabalho em 11 horas e 12 minutos.
Trabalhando em conjunto, eles conseguem assentar
Em uma hora eles conseguem assentar
11,2 horas equivalem a 11 horas e 12 minutos, as 11 horas correspondem à parte inteira e os 12 minutos à parte fracionária multiplicada por 60, já que temos 60 minutos em uma hora.
Então:
Trabalhando juntos, os assentadores conseguem realizar tal trabalho em 11 horas e 12 minutos.7) Para comprar um certo brinquedo, da quantia necessária João possui um terço e Maria possui um quarto. Dona Lurdes, a mãe deles, prometeu completar com os R$ 125,00 que faltam para eles completarem o valor. Quanto custa tal brinquedo? Se dividirmos a fração referente aos R$ 125,00 que serão fornecidos por Dona Lurdes, iremos encontrar justamente o valor do brinquedo, mas que fração é esta?
Sabemos que 1 corresponde ao valor total do brinquedo, desta forma se dele subtraímos a fração referente à parte de João, juntamente com a parte de Maria, teremos a parte referente aos R$ 125,00 que faltam:
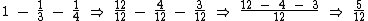
Como dito, ao dividirmos R$ 125,00 por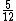 iremos descobrir quanto custa o tal brinquedo:
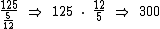
Desta forma:
Tal brinquedo custa R$ 300,00.
Sabemos que 1 corresponde ao valor total do brinquedo, desta forma se dele subtraímos a fração referente à parte de João, juntamente com a parte de Maria, teremos a parte referente aos R$ 125,00 que faltam:
Como dito, ao dividirmos R$ 125,00 por
Desta forma:
Tal brinquedo custa R$ 300,00.8) Para transportar uma determinada carga, um caminhão A precisa de quatro viagens e um caminhão B precisa de cinco viagens. Trabalhando em conjunto com um caminhão C, eles conseguem transportar a carga em apenas duas viagens. Quantas viagens o caminhão C precisaria para transportar esta carga sozinho? Como sempre 1 representa o todo, neste caso equivale a toda a carga.
Como em conjunto os três caminhões fazem apenas duas viagens, em cada uma delas eles levam metade da carga (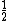
).
Segundo este mesmo raciocínio, o caminhão A transporta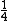
da carga por viagem, assim como o caminhão B transporta 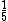. Subtraindo de 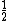estas duas frações temos:
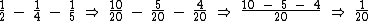
Ou seja, em cada viagem o caminhão C transporta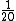
da carga.
Concluímos então que para transportar toda a carga, o caminhão C precisaria de 20 viagens, que podemos calcular simplesmente dividindo 1 por: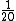
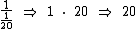
Então:
O caminhão C precisaria de 20 viagens para transportar esta carga sozinho.
Como em conjunto os três caminhões fazem apenas duas viagens, em cada uma delas eles levam metade da carga (
Segundo este mesmo raciocínio, o caminhão A transporta
Ou seja, em cada viagem o caminhão C transporta
Concluímos então que para transportar toda a carga, o caminhão C precisaria de 20 viagens, que podemos calcular simplesmente dividindo 1 por
Então:
O caminhão C precisaria de 20 viagens para transportar esta carga sozinho.9) Um feirante vendeu metade das trezentas dúzias de laranjas que comprou, a R$ 2,00 a dúzia. Dois terços da outra metade vendeu a R$ 1,50 a dúzia e o restante vendeu a R$ 1,00 a dúzia. Qual é a fração das dúzias correspondentes a cada valor de venda e quanto o vendedor faturou na venda? A fração correspondente ao preço de R$ 2,00 tiramos diretamente do enunciado: .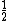
A fração correspondente ao preço de R$ 1,50 é obtido calculando-s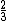e
de :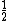
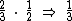
Se de 1, a fração correspondente às 300 dúzias, subtrairmos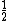 correspondente as laranjas vendidas a R$ 2,00 a dúzia e também 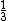correspondente as laranjas vendidas a R$ 1,50 a dúzia, encontraremos a fração que foi vendida a um real a dúzia:
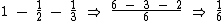
Agora ao somarmos os produtos do número total de dúzias por cada uma das frações multiplicada por seus respectivos valores da dúzia, teremos o valor total faturado:
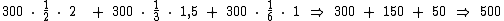
Portanto:
Na venda o feirante faturou R$ 500,00, sendo que 1/2 das 300 dúzias foram vendidas a R$ 2,00 a dúzia, 1/3 a R$ 1,50 a dúzia e 1/6 a R$ 1,00 a dúzia.
A fração correspondente ao preço de R$ 1,50 é obtido calculando-se
Se de 1, a fração correspondente às 300 dúzias, subtrairmos
Agora ao somarmos os produtos do número total de dúzias por cada uma das frações multiplicada por seus respectivos valores da dúzia, teremos o valor total faturado:
Portanto:
Na venda o feirante faturou R$ 500,00, sendo que 1/2 das 300 dúzias foram vendidas a R$ 2,00 a dúzia, 1/3 a R$ 1,50 a dúzia e 1/6 a R$ 1,00 a dúzia.10) Cinco oitavos de três sétimos do valor de uma multa de trânsito que Zeca pé de chumbo recebeu, é igual a R$ 75,00. Qual é o valor da multa de trânsito referente à infração que Zeca pé de chumbo cometeu? Este problema é bastante simples, basta refazermos as contas em ordem inversa. Primeiro dividimos R$ 75,00 por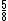 
e depois dividimos por 
:
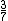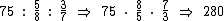
Logo:
O valor da multa de trânsito referente à infração é de R$ 280,00.
Logo:
O valor da multa de trânsito referente à infração é de R$ 280,00. Referências:
http://www.matematicadidatica.com.br/FracaoExercicios.aspx#anchor_ex10
http://www.somatematica.com.br
Nenhum comentário:
Postar um comentário