Limites
Definição 2.1.1 Dados uma função  e um ponto de acumulação a de B, diz-se que um número
e um ponto de acumulação a de B, diz-se que um número  é limite de f em a, e se escreve:
é limite de f em a, e se escreve:

quando vale a seguinte condição: Para todo , existe
, existe  tal que:
tal que:
Daremos preferência à primeira notação. quando vale a seguinte condição: Para todo
Não podemos abrir mão da condição de a ser ponto de acumulação de B, pois é ela que reflete a nossa idéia intuitiva inicial de que a possa ser aproximado por pontos de B distintos de a.
A definição de limite pode ser parafrazeada nos seguintes termos:
Definição 2.1.2 Dados uma função  e um ponto de acumulação a de B, diz-se que
e um ponto de acumulação a de B, diz-se que  é o limite de f em a, se para todo
é o limite de f em a, se para todo  existe
existe  satisfazendo:
satisfazendo:
Observação 2.1.1 Notemos que não importa quão pequeno seja o número  dado; se
dado; se  , é sempre possível encontrar
, é sempre possível encontrar  de modo que a relação (2.1) valha.
de modo que a relação (2.1) valha.
Vamos analisar a Definição 2.1.1 num caso concreto. Consideremos a função 
Note que f não está definida no ponto x=1. No entanto, para
|f(x)-4|=|2(x+1)-4|=2|x-1|.
Assim, dado
ou seja,
Com o exemplo acima e os que damos a seguir visamos exclusivamente clarificar a definição de limite. O objetivo de um curso de Cálculo não pode ser o de aprender a calcular limites usando a Definição 2.1.1. Daqui a pouco aprenderemos algumas propriedades que permitem ver, por exemplo, que
Exemplo 2.1.1 (1) Se considerarmos f(x)=c (constante), temos talvez o exemplo mais simples deste capítulo:

Conferindo a definição de limite, dado , qualquer número
, qualquer número  se ajusta ao nosso objetivo, pois sempre teremos
se ajusta ao nosso objetivo, pois sempre teremos  . (2) Se f(x)=x, temos
. (2) Se f(x)=x, temos  . De fato, dado
. De fato, dado  , se tomarmos
, se tomarmos  temos a relação (2.1) imediatamente satisfeita com
temos a relação (2.1) imediatamente satisfeita com  .
.
(3) . De fato, dado
. De fato, dado  , para encontrar um
, para encontrar um  que nos convenha, notemos que neste caso a=2 e
que nos convenha, notemos que neste caso a=2 e  . Assim, se tomarmos
. Assim, se tomarmos  , temos:
, temos:

(4) . De fato, dado
. De fato, dado  , vamos procurar
, vamos procurar  sob a restrição
sob a restrição  . Assim,
. Assim,  implica 1<x<3 e, portanto, |x+2|<5. Logo, se
implica 1<x<3 e, portanto, |x+2|<5. Logo, se  , temos
, temos

Portanto, basta tomar . (5)
. (5)  . De fato, observemos que sempre
. De fato, observemos que sempre  ; confira com a Figura 2.1.1 Assim, dado
; confira com a Figura 2.1.1 Assim, dado  , podemos tomar
, podemos tomar  uma vez que, neste caso:
uma vez que, neste caso:

(6) . A justificativa é inteiramente análoga à do exemplo anterior.
. A justificativa é inteiramente análoga à do exemplo anterior.
Uma consequência da Definição é 2.1.1 a unicidade do limite. Conferindo a definição de limite, dado
(3)
(4)
Portanto, basta tomar
(6)
Proposição 2.1.1 Seja  e suponhamos que exista o limite de f em um ponto a. Então ele é único.
e suponhamos que exista o limite de f em um ponto a. Então ele é único.
Prova Suponhamos que Escolhendo
Da arbitrariedade de
Exemplo 2.1.2 (1)  não existe. De fato, seja f(x)=x/|x|. Como f(x)=1, para x>0, se existisse
não existe. De fato, seja f(x)=x/|x|. Como f(x)=1, para x>0, se existisse  teriamos
teriamos  . De modo análogo verificar-se-ia
. De modo análogo verificar-se-ia  . Assim, os números 1 e -1 teriam de ser iguais a
. Assim, os números 1 e -1 teriam de ser iguais a  contrariando a unicidade do limite. (2)
contrariando a unicidade do limite. (2)  não existe. De fato, suponhamos, por contradição, que exista
não existe. De fato, suponhamos, por contradição, que exista  . Dado
. Dado  , digamos,
, digamos,  , deve existir
, deve existir  tal que
tal que

Portanto, se ,
,
Mas, se e
e  ,
,  , temos
, temos  e
e  (veja o gráfico da função
(veja o gráfico da função  , para x>0, na figura a seguir). Observe, entretanto, que para
, para x>0, na figura a seguir). Observe, entretanto, que para  suficientemente grande temos
suficientemente grande temos

o que contraria a condição (2.7). Logo, não existe .
.
Portanto, se
Mas, se
o que contraria a condição (2.7). Logo, não existe
O item (1) do Exemplo 2.1.2 sugere um outro tipo de limite mais restrito, o limite à esquerda e o limite à direita: são os limites laterais. Para definir esses conceitos precisamos da noção de ponto de acumulação lateral, isto é,
Definição 2.1.3 Consideremos um ponto  e um conjunto
e um conjunto  . Diz-se que a é um ponto de acumulação lateral de B, deixando B à esquerda, se a é ponto de acumulação de
. Diz-se que a é um ponto de acumulação lateral de B, deixando B à esquerda, se a é ponto de acumulação de ![$B\bigcap(-\infty,a]$](http://www.icmc.usp.br/%7Epztaboas/nocte/img299.gif) . Define-se analogamente ponto de acumulaçao lateral de um conjunto
. Define-se analogamente ponto de acumulaçao lateral de um conjunto  , deixando B à direita.
, deixando B à direita.
É claro que um ponto de acumulação lateral de um conjunto Podemos agora definir limite à esquerda de f em a em termos da restrição
Definição 2.1.4 Consideremos uma função  , e seja a um ponto de acumulação lateral de
, e seja a um ponto de acumulação lateral de  , deixando B à esquerda. O limite à esquerda de f em a é
, deixando B à esquerda. O limite à esquerda de f em a é  , se
, se ![$\lim_{x\to a}{f\vert}_{(-\infty,a]\cap B}(x)=\ell$](http://www.icmc.usp.br/%7Epztaboas/nocte/img301.gif) .
.
Denota-se: Observação 2.1.2 Suponhamos que a seja ponto de acumulação lateral de  , deixando B à esquerda e à direita simultaneamente. Se existir o limite
, deixando B à esquerda e à direita simultaneamente. Se existir o limite  de uma função
de uma função  , então existem ambos os limites laterais de f em a, mas a recíproca é falsa, como mostra o item (1) do exemplo 2.1.2.
, então existem ambos os limites laterais de f em a, mas a recíproca é falsa, como mostra o item (1) do exemplo 2.1.2.
Observação 2.1.3 Suponhamos que as condições assumidas na definição dos limites laterais de f, quando  se cumpram. Neste caso, existe o limite
se cumpram. Neste caso, existe o limite  de f em a se, e somente se, existem os dois limites laterais e ambos são iguais a
de f em a se, e somente se, existem os dois limites laterais e ambos são iguais a  , isto é,
, isto é,

Confira com o Exercício 7.
Embora quase inocente, a observação anterior é um bom recurso em muitas situações práticas. No item (1) do Exemplo 2.1.2 temos Confira com o Exercício 7.
porisso concluimos que o limite em questão não existe. Mais adiante, na demonstração do Teorema do Primeiro Limite Fundamental esse recurso será utilizado positivamente, isto é, para mostrar que um certo limite existe. Daqui em diante proporemos alguns exercícios mais práticos, visando treinar a manipulação das técnicas, e outros mais conceituais, procurando fixar as idéias importantes da teoria. O leitor deve se sentir desafiado por qualquer um que lhe inspire dificuldade.
EXERCÍCIOS
I - Calcule, caso existam, os limites abaixo. Se não existirem, determine a tendência da imagem ou justifique a não existência:
1. 
 2.
2. 
 3.
3. 

4.
 5.
5. 
 6.
6. 

7.
 8.
8. 
 9.
9.

10. 
 11.
11.
 12.
12.

13. 
 14.
14.
 15.
15.

16. 
 17.
17. f(x) sendo f(x) =
f(x) sendo f(x) =

18.  f(x) sendo f(x) =
f(x) sendo f(x) = 

RESPOSTAS
1)9/4 2) 2/3 3) 2 4) –1 5)  6) 0 7)
6) 0 7)  8) 3/2 9) 0 10) +
8) 3/2 9) 0 10) +
11) + 12)
12)  13) –1 14) NE 15) 1/5 16) NE 17) NE 18) 1
13) –1 14) NE 15) 1/5 16) NE 17) NE 18) 1
II - Seja a função f definida por f(x)=  Verifique se f é contínua nesse intervalo.
Verifique se f é contínua nesse intervalo.
III - Seja a função f definida por f(x) =  . Calcule m para que f seja contínua em zero.
. Calcule m para que f seja contínua em zero.
 . Calcule m para que f seja contínua em zero.
. Calcule m para que f seja contínua em zero.IV – Sabendo que f dada por f(x) =  para
para  e
e  , é uma função contínua em zero, calcule f(0).
, é uma função contínua em zero, calcule f(0).
V - A função f definida por f(x) =  é contínua em 3 ? Justifique.
é contínua em 3 ? Justifique.
 é contínua em 3 ? Justifique.
é contínua em 3 ? Justifique.VI - Sendo f a função definida por f(x) =  verifique:
verifique:
 verifique:
verifique:a) se f é contínua em 1. Justifique.
b) se f é contínua em 0. Justifique.
VII - Esboce o gráfico cartesiano de uma função f que satisfaça simultaneamente as seguintes condições:
a) Dom f = IR
b) f apresenta uma descontinuidade essencial em 0;
c) f apresenta uma descontinuidade removível no 2 ;
d)  f(x) = 0
f(x) = 0
e)  f(x) = +
f(x) = +
RESPOSTAS:
II) Sim III) m = 5/8 IV) 4 V) Não VI) a) Sim b) Não
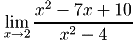 | |
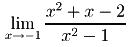 | |
 | |
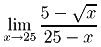 | |
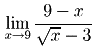 | |
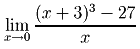 | |
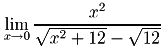 | |
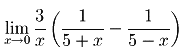 | |
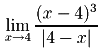 | |
 | |
REFERÊNCIAS:
http://www.mtm.ufsc.br/~azeredo/calculos/Acalculo/x/listas/limites/limite.html
http://www.pucrs.br/famat/silveira/calculoa/m1/m1_lista2.htm
http://www.feg.unesp.br/~gsena/Orientacoes_Academicas/P%E1gina%20Pessoal/Exercicios%20resolvidos%20-%20limites.html#ex11
http://pt.scribd.com/doc/266877/Exercicios-resolvidos-de-calculo-I
http://www.slideshare.net/fernandoribeirao/lista-de-exercicios-limites
http://www.cmjf.com.br/cmjf24horas/aluno/arq_clubes/1180141663.pdf
http://pt.wikipedia.org/wiki/Limite
http://ginasiomental.com/material/12/limites.pdf
http://pessoal.sercomtel.com.br/matematica/superior/calculo/limites/limites.htm



![\begin{displaymath}
f\bigl([V_\delta(c)\setminus\{c\}]\cap B\bigr)\subset V_\varepsilon(\ell)
\end{displaymath}](http://www.icmc.usp.br/%7Epztaboas/nocte/img240.gif)




Nenhum comentário:
Postar um comentário