Confira clicando no link
Boa Pesquisa!
Número Primos
"Wikipédia"
Um número natural é um número primo quando ele tem exatamente dois divisores: o número um e ele mesmo[1].
Nos inteiros,  é um primo se ele tem exatamente quatro divisores:
é um primo se ele tem exatamente quatro divisores: 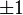 e
e 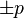 . Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
. Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
 é um primo se ele tem exatamente quatro divisores:
é um primo se ele tem exatamente quatro divisores: 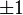 e
e 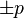 . Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
. Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.Existem infinitos números primos, como demonstrado por Euclides por volta de 300 a.C..
A propriedade de ser um primo é chamada "primalidade", e a palavra "primo" também é utilizada como substantivo ou adjetivo. Como "dois" é o único número primo par, o termo "primo ímpar" refere-se a todo primo maior do que dois.
Se um número inteiro tem módulo maior que um e não é primo, diz-se que é composto. Por convenção, os números 0, 1 e -1 não são considerados primos nem compostos.
O conceito de número primo é muito importante na teoria dos números. Um dos resultados da teoria dos números é o Teorema Fundamental da Aritmética, que afirma que qualquer número natural diferente de 1 pode ser escrito de forma única (desconsiderando a ordem) como um produto de números primos (chamadosfatores primos): este processo se chama decomposição em fatores primos (fatoração).
Os 100 primeiros números primos positivos são:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541
Exemplos de decomposições:
Assista aos vídeos
Os átomos da aritmética
Os gregos foram os primeiros a perceber que qualquer número natural, exceto o 1, pode ser gerado pela multiplicação de números primos, os chamados blocos de construção". A primeira pessoa, até onde se sabe, que produziu tabelas de números primos foi Eratóstenes, no terceiro século a.C. Ele escrevia inicialmente uma lista com todos os números de 1 a 1000. Em seguida escolhia o primeiro primo, 2, e eliminava da lista todos os seus múltiplos. Passava ao número seguinte que não fora eliminado e procedia também eliminando todos os seus múltiplos. Desta forma Erastótenes produziu tabelas de primos, mais tarde este procedimento passou a se chamar de crivo de Eratóstenes.
Durante o século XVII os matemáticos descobriram o que acreditavam ser um método infalível para determinar se um número N era primo: calcule 2 elevado a potência N e divida-o por N, se o resto for 2, então o número será primo. Em termos da calculadora-relógio de Gauss, esses matemáticos estavam tentando calcular 2N em um relógio com N horas. Em 1819, o teste dos números primos foi eliminado, pois funciona para todos os números até 340, mas falha para  . Exceção descoberta com uma calculadora-relógio de Gauss contendo 341 horas utilizada para simplificar a análise de um número como2341.
. Exceção descoberta com uma calculadora-relógio de Gauss contendo 341 horas utilizada para simplificar a análise de um número como2341.
 . Exceção descoberta com uma calculadora-relógio de Gauss contendo 341 horas utilizada para simplificar a análise de um número como2341.
. Exceção descoberta com uma calculadora-relógio de Gauss contendo 341 horas utilizada para simplificar a análise de um número como2341.Teoremas dos números primos
Existem vários teoremas e estudos sobre os números primos, desde resultados tratados na matemática elementar, até conjecturas que não foram provadas.
Matemática elementar
Alguns resultados que podem ser demonstrados com ferramentas elementares (para ver as demonstrações, consulte Vianna[1]):
- Se um número primo divide um produto, mas não divide um dos fatores, então ele divide o outro fator
- Se um número primo divide a potência de outro número, então ele divide este número
- Se um número é múltiplo, então ele tem pelo menos um fator primo
Teoria dos números
Sabe-se que, à medida que avançamos na seqüência dos números inteiros, os primos tornam-se cada vez mais raros. Isto levanta duas questões:
- O conjunto dos números primos seria finito ou infinito?
- Dado um número natural n, qual é a proporção de números primos entre os números menores que n?
- A resposta à primeira questão é que o conjunto dos primos é infinito, um resultado conhecido na parte central dos Elementos de Euclides, que lida com as propriedades dos números. Na proposição 20, Euclides explica uma verdade simples porém fundamental sobre os números primos: existe um número infinito deles. Pode-se demonstrar, em notação moderna, da seguinte forma:
- Suponha, por absurdo, que o número de primos seja finito e sejam
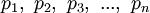 os primos. Seja P o número tal que
os primos. Seja P o número tal que
-
- P =
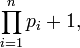 onde
onde  denota o produtório.
denota o produtório.
- P =
- Se P é um número primo, é necessariamente diferente dos primos
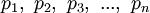 , pois sua divisão por qualquer um deles tem um resto de 1.
, pois sua divisão por qualquer um deles tem um resto de 1.
- Por outro lado, se P é composto, existe um número primo q tal que q é divisor de P.
- Mas obviamente
 Logo existe um novo número primo.
Logo existe um novo número primo.
- Há um novo número primo, seja P primo ou composto; este processo pode ser repetido indefinidamente, logo há um número infinito de números primos.
- Uma outra prova envolve considerar um número inteiro n > 1. Temos n + 1 que, necessariamente, é coprimo de n (números coprimos são os que não têm nenhum fator comum maior do que 1). Provamos isto imaginando que a divisão do menor pelo maior tem resultado 0 e resto n e do maior pelo menor tem resultado 1 e resto 1. Assim, n(n + 1) tem, necessariamente, ao menos dois factores primos.
- Tomemos o sucessor deste, que representamos como n(n + 1) + 1. Pelo mesmo raciocínio, ele é coprimo a n(n + 1). Ao multiplicar os dois números, temos [n(n + 1)] * [n + (n + 1) + 1]. Como um de seus fatores tem pelo menos dois factores primos diferentes e é coprimo ao outro, o resultado da multiplicação tem pelo menos três factores primos distintos. Este raciocínio também pode ser infinitamente estendido.
- A resposta para a segunda pergunta acima é que essa proporção é aproximadamente
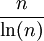 , onde ln é o logaritmo natural.
, onde ln é o logaritmo natural.
- Para qualquer inteiro k, existem k inteiros consecutivos todos compostos.
- O produto de qualquer sequência de k inteiros consecutivos é divisível por k!
- Se k não é primo, então k possui, necessariamente, um fator primo menor do que ou igual a
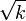 .
.
- Todo inteiro maior que 1 pode ser representado de maneira única como o produto de fatores primos
Grupos e sequências de números primos
Pierre de Fermat (1601-1665) descobriu que todo número primo da forma 4n + 1, tal como 5,13,17,29,37,41, etc., é a soma de dois quadrados. Por exemplo:
- 5 = 12 + 22,
- 13 = 22 + 32,
- 17 = 12 + 42,
- 29 = 22 + 52,
- 37 = 12 + 62,
- 41 = 42 + 52.
Hoje são conhecidos dois grupos de números primos:
- (4n + 1) - que podem sempre ser escritos na forma (x2 + y2);
- e (4n − 1) - nunca podem ser escritos na forma (x2 + y2).
Tratando-se de números primos é perigoso fazer uma generalização apenas com base numa observação, não solidamente comprovada matematicamente. Vejamos o exemplo: 31, 331, 3.331, 33.331, 333.331, 3.333.331 e 33.333.331 são primos mas 333.333.331 não é, pois (333.333.331 = 17 x 19.607.843).
Um olhar mais atento na forma como se distribuem os números primos revela que não há uma regularidade nesta distribuição. Por exemplo existem longosburacos entre os números primos, o número 370.261 é seguido de cento e onze[2] números compostos e não existem[3] primos entre os números 20.831.323 e 20.831.533. Essa irregularidade na distribuição dos números primos é uma das razões[carece de fontes] de não existir uma fórmula matemática que produza todos os números primos[carece de fontes]. Algumas fórmulas produzem muitos números primos, por exemplo x2 − x + 41 fornece primos quando 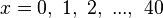 [4][5]. Veja que para x = 41, a fórmula resulta em 412 que não é primo.
[4][5]. Veja que para x = 41, a fórmula resulta em 412 que não é primo.
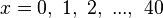 [4][5]. Veja que para x = 41, a fórmula resulta em 412 que não é primo.
[4][5]. Veja que para x = 41, a fórmula resulta em 412 que não é primo.Não existe uma fórmula que forneça primos para todos os valores primos de x, de fato em 1.752 Goldbach provou que não há uma expressão polinomial em x com coeficientes inteiros que possa fornecer primos para todos os valores de x.
Não se sabe se há uma expressão polinomial ax2 + bc + c com  que represente infinitos números primos. Dirichlet usou métodos para provar que se a,2b e c não têm fator primo em comum, a expressão polinomial a duas variáveis
que represente infinitos números primos. Dirichlet usou métodos para provar que se a,2b e c não têm fator primo em comum, a expressão polinomial a duas variáveis
 que represente infinitos números primos. Dirichlet usou métodos para provar que se a,2b e c não têm fator primo em comum, a expressão polinomial a duas variáveis
que represente infinitos números primos. Dirichlet usou métodos para provar que se a,2b e c não têm fator primo em comum, a expressão polinomial a duas variáveis- ax2 + 2bxy + cy2
representa infinitos primos, quando x e y assumem valores positivos inteiros.
Fermat pensou que a fórmula 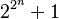 forneceria números primos para
forneceria números primos para 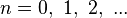 . Este números são chamados de números de Fermat e são comumente denotados por Fn. Os cinco primeiros números são:
. Este números são chamados de números de Fermat e são comumente denotados por Fn. Os cinco primeiros números são:
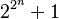 forneceria números primos para
forneceria números primos para 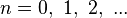 . Este números são chamados de números de Fermat e são comumente denotados por Fn. Os cinco primeiros números são:
. Este números são chamados de números de Fermat e são comumente denotados por Fn. Os cinco primeiros números são: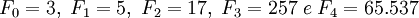 ,
,
sendo todos primos.
Maior número primo conhecido
Atualmente o maior número primo encontrado é 243.112.609 − 1 descoberto no dia 23 de agosto de 2008, num projeto de computação distribuída pela Internet, oGIMPS, que usa o tempo ocioso do processador de computadores pessoais, procurando por números primos específicos, do tipo 2p − 1, em que p é primo, chamados primos de Mersenne. Este último primo encontrado é o primo de Mersenne de número 46 e tem 12.978.189 dígitos.
Aproximações para o n-ésimo primo
Como consequência do teorema do número primo , uma expressão assintótica para o n-ésimo primo pn é:
- pn˜nlnn.
Uma aproximação melhor é:
O teorema de Rosser mostra que pn é maior que n ln n. É possível melhorar esta aproximação com os limites [7][8]:







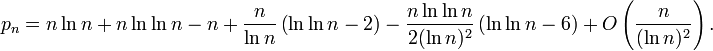

Nenhum comentário:
Postar um comentário